Solve the given differential equation

[chwala]

Homework Statement

See attached.

Relevant Equations

separation of variables

I am on differential equations today...refreshing.

Ok, this is a pretty easier area to me...just wanted to clarify that the constant may be manipulated i.e dependant on approach. Consider,

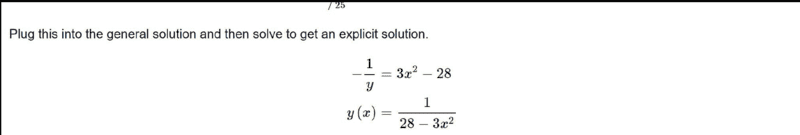
Ok I have,

$\dfrac{dy}{6y^2}= x dx$

on integration,

$-\dfrac{1}{6y} + k = \dfrac{x^2}{2}$

$k= \dfrac{x^2}{2} + \dfrac{1}{6y}$

using $y(1)=0.04$ we shall get,

$k=\dfrac{28}{6}$

$\dfrac{28}{6}-\dfrac{x^2}{2}=\dfrac{1}{6y}$

...

aaargh looks like i will get the same results...cheers

 

[Mark44]

So, you don't have a problem, right?

 

[chwala]

So, you don't have a problem, right?

Correct, I do not have a problem.

Where one places the constant doesn't really matter in these kind of problems.

 

[Mark44]

Where one places the constant doesn't really matter in these kind of problems.

It does matter in certain cases.
If I worked the problem like this ...
$\frac {dy}{y^2} = 6x~dx$
$\frac{-1}y = 3x^2$ (Omitting the constant for now)
$y = \frac{-1}{3x^2} + C$ (Adding the constant now)

The above gives the wrong value for C when you substitute in the initial condition.
I'm not saying that's what you meant. In the second line above, you could write it as $\frac{-1}y = 3x^2 + C_1$ or as $\frac{-1}y + C_2= 3x^2$.
The constants will be different, but when you solve for y in either equation, the solutions will be the same.

$\dfrac{28}{6}-\dfrac{x^2}{2}=\dfrac{1}{6y}$

You should write the solution in the form y = f(x), as was shown in the solution.

 

[chwala]

It does matter in certain cases.
If I worked the problem like this ...
$\frac {dy}{y^2} = 6x~dx$
$\frac{-1}y = 3x^2$ (Omitting the constant for now)
$y = \frac{-1}{3x^2} + C$ (Adding the constant now)

The above gives the wrong value for C when you substitute in the initial condition.
I'm not saying that's what you meant. In the second line above, you could write it as $\frac{-1}y = 3x^2 + C_1$ or as $\frac{-1}y + C_2= 3x^2$.
The constants will be different, but when you solve for y in either equation, the solutions will be the same.

You should write the solution in the form y = f(x), as was shown in the solution.

@Mark44 I realized that it would just give the same solution, thus left it hanging.