Solve the inequality problem that involves modulus

[chwala]

Homework Statement

See attached

Relevant Equations

modulus

This is the question * consider the highlighted question only *with its solution shown (from textbook);

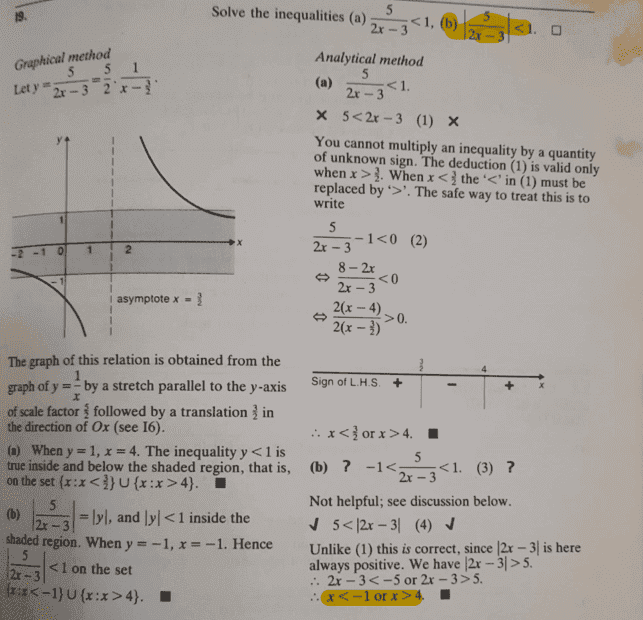
My approach is as follows (alternative method),
$|\frac {5}{2x-3}|$< $1$
Let, $\frac {5}{2x-3}$⋅$\frac {5}{2x-3}$=$1$
→$x^2-3x-4=0$
$(x+1)(x-4)=0$
it follows that the critical values are $x_1=-1$ and $x_2=4$, which will give the correct solution once we confirm/establish the valid region in the given inequality.
Is their another method on this type of questions? ... regards

 

[anuttarasammyak]

$$5<|2x-3|$$
$$5/2<|x-3/2|$$
$$x-3/2<-5/2, \ 5/2<x-3/2$$
$$x<-1, \ 4<x$$

 

[chwala]

$$5<|2x-3|$$
$$5/2<|x-3/2|$$
$$x-3/2<-5/2, \ 5/2<x-3/2$$
$$x<-1, \ 4<x$$

Nice one, I will write this in my notebook ...good way to simplify ...$ax...$

 

[Mark44]

$5<|2x-3|$
$5/2<|x-3/2|$
$x-3/2<-5/2, \ 5/2<x-3/2$
$x<-1, \ 4<x$

The use of commas in the last two lines implies "and", which can't happen here, as it's impossible for x to be both less than -1 and larger than 4.
Here's how I would write this:
$|2x - 3| > 5$
$2x - 3 > 5 \text{ or } 2x - 3 < -5$
$2x > 8 \text{ or } 2x < -2$
$x > 4 \text{ or } x < -1$

 

[chwala]

Thanks Mark...a learning point for me too...

The use of commas in the last two lines implies "and", which can't happen here, as it's impossible for x to be both less than -1 and larger than 4.
Here's how I would write this:
$|2x - 3| > 5$
$2x - 3 > 5 \text{ or } 2x - 3 < -5$
$2x > 8 \text{ or } 2x < -2$
$x > 4 \text{ or } x < -1$