rayj098
- 8
- 0
Homework Statement
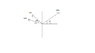
10.0km [N] + 5.0km [E15S]
Homework Equations
Cosine Law
The Attempt at a Solution
If you draw it out you see that 10km is 90 degrees north. From the 10km end, you do E15S for 5km.
Therefore, a = 10km, b = 5km, c = ?, C = 90 - 15 = 75.
Therefore:
c^2 = 10^2 + 5^2 - 2(10)(5) Cos 75
c^2 = 99.12
c = 9.9
Sin Law to find the angle of the resultant
Sin A = Sin B
----- ------
a = b
Sin 75 Sin B
------- = -------
9.9 5
B = 29
So final answer is 9.9km [N29E]
Somehow the answer is 4.2[N35E]...