I Solving 2 equations and 2 unknowns with vectors

[matt382]

Hi, I have a work-related problem to solve and I'm not sure where to start and a pointer would be appreciated. I have the following two sets of polar equations

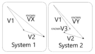
V1 + V2 = Vx
V1 + V2 + V3 = Vy,

where Vx, V3, and Vy have been measured with reasonable accuracy, maybe +/-2%

Any thoughts on how to approach? If, for example, if I convert to rectangular form and try substitution the entire thing is quickly swimming in a sea of sines and cosines that cannot possibly be solvable

My question is this: There should be enough known to solve, is that right? Can this just go into a matrix and get solved that way?

thanks for any help

 

[BvU]

hello matt,
looks like you do not have enough to solve: all you have is 2 measurements of v1+v2

 

[fresh_42]

The equations don't allow you to separate $V1$ from $V2$. You could set $V1+V2=:U$ and have the same amount of information coded. There is no way to achieve the values of $V1$ or $V2$.

 

[matt382]

Hi BvU and fresh_42, I understand your point if they were scalar numbers. But it intuitively feels to me that because these are vectors that there's an additional constraint present in the form of angles that must be achieved.

In the attached, with System 1 of course V1 and V2 have an infinite solution space. But look at System 2: Visually it appears to be completely constrained. If you change the position of V3, then you will break the system 1 constraint that V1 and V2 have a fixed angle between them, for example. And we know both VX and VY. In other words, this looks completely constrained to me--there's no other way to draw the vectors when both systems are considered.

Am I just not seeing this correctly?

 

[fresh_42]

No. You need an equation which makes two variables. You have only one variable: $U=V1+V2$. Often $V1-V2$ does the job, but I don't know your system and whether you can measure the difference.

 

[HallsofIvy]

You have one equation that says V1+ V2= VX and another that says V1+ V2= VY- V3, with VX, VY, and V3 known. If VX= VY- V3 then there are infinitely many solutions. If they are not equal, there is no solution.

 

[fresh_42]

You have one equation that says V1+ V2= VX and another that says V1+ V1= VY- V3, with VX, VY, and V3 known. If VX= VY- V3 then there are infinitely many solutions. If they are not equal, there is no solution.

The situation has two unknowns $x=V1$ and $y=V2$, and two known variables $a=VX$ and $b=VY-V3\,.$ The equations now read $x+y=a$ and $2x=b$. This can always uniquely be solved.

 

[BvU]

That's just a typo !