Mech King
- 69
- 0
Hello,
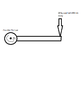
I think i may be over analyzing this basic problem, but if i have a lever similar to that attached, and i apply a load at one end and a counter moment at the over end (at the pivot center) to balance the load then the system is in equilibrium.
Now if the load applied on the end of lever was not parrallel with gravity, but perpendicular to it, so the image attached became a tope view as opposed to a side view, then how do you quantify the torque, because although gravity is always present, it now won't be tending to push the load around anti-clockwise, so how can i equate the load to a force and resolve this problem? Clearly, if the attached image shows a top/plan view of the system then the lever will be easier to turn.
Can someone please help me understand my madness?
Cheers
I think i may be over analyzing this basic problem, but if i have a lever similar to that attached, and i apply a load at one end and a counter moment at the over end (at the pivot center) to balance the load then the system is in equilibrium.
Now if the load applied on the end of lever was not parrallel with gravity, but perpendicular to it, so the image attached became a tope view as opposed to a side view, then how do you quantify the torque, because although gravity is always present, it now won't be tending to push the load around anti-clockwise, so how can i equate the load to a force and resolve this problem? Clearly, if the attached image shows a top/plan view of the system then the lever will be easier to turn.
Can someone please help me understand my madness?
Cheers