Solving a Constant Acceleration Problem: Help from Phil

AI Thread Summary
To solve the constant acceleration problem, start by applying the equations of motion for uniformly accelerated motion. Given the initial speed of 4 m/s and a constant acceleration of 2 m/s², calculate the time to reach point B using the formula for velocity and acceleration. Consider both tangential and centripetal acceleration components, as the motion involves circular dynamics. Identifying relevant equations, such as those for circular motion, will help in relating the concepts effectively. The solution requires a clear understanding of the relationship between linear and circular motion principles.
truetaurus
Messages
2
Reaction score
0
I got the following question:

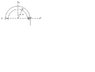
When the car reaches point A it has a speed of 4 m/s, which is increasing at a constant rate of 2 m/s2. Determine the time required to reach point B and the magnitudes of its velocity and acceleration.


See attachment for how the diagram looks like.

Now i am not sure how to go about solving this? I have worked out the arc of the half circle but now what?

thanks
phil
 

Attachments

  • Question Diagram.jpg
    Question Diagram.jpg
    4.4 KB · Views: 393
Physics news on Phys.org
concepts involved in this problem:
uniform circular motion
tangential acceleration and velocity
centripetal acceleration due to uniform circular motion
 
ya i know that, but I am stuck where i can start from?
 
perhaps the next step is to identify potentially relevant equations and see if they give you a hint as to how to relate the concepts.
 

Thread 'Errors and significant figures'

I multiplied the values first without the error limit. Got 19.38. rounded it off to 2 significant figures since the given data has 2 significant figures. So = 19. For error I used the above formula. It comes out about 1.48. Now my question is. Should I write the answer as 19±1.5 (rounding 1.48 to 2 significant figures) OR should I write it as 19±1. So in short, should the error have same number of significant figures as the mean value or should it have the same number of decimal places as...
View full post »
Thread 'A cylinder connected to a hanging mass'

Thread 'A cylinder connected to a hanging mass'

Let's declare that for the cylinder, mass = M = 10 kg Radius = R = 4 m For the wall and the floor, Friction coeff = ##\mu## = 0.5 For the hanging mass, mass = m = 11 kg First, we divide the force according to their respective plane (x and y thing, correct me if I'm wrong) and according to which, cylinder or the hanging mass, they're working on. Force on the hanging mass $$mg - T = ma$$ Force(Cylinder) on y $$N_f + f_w - Mg = 0$$ Force(Cylinder) on x $$T + f_f - N_w = Ma$$ There's also...
View full post »

Similar threads

Problem with the power of car
Replies
3
Views
810
Terminal velocity and acceleration
Replies
7
Views
884
In a constant acceleration motion, Is it possible to have constant speed?
Replies
11
Views
1K
Kinematics: Acceleration of a figure skater changing direction
Replies
16
Views
1K
Why would this be accelerating positively?
Replies
6
Views
912
Relation between Friction, Velocity, and Acceleration
Replies
16
Views
923
Relating acceleration to distance and time
Replies
5
Views
3K
Help with question on motion: Avoiding a rear-end collision
Replies
6
Views
3K
Is My Calculation of Centripetal Acceleration and Tangential Velocity Correct?
Replies
12
Views
1K
Non-constant acceleration, solving for velocity
Replies
11
Views
2K

Hot Threads

Recent Insights

Back
Top