Solving a Pin Joint System with Vertical Load

[sriram123]

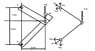
Hi all,I just started to learn mechanics so please forgive me if i ask something elementary.I have an example from Egor P Popov's Engineering mechanics of solids.(Please refer attachment and sorry about quality of drawing).

This is a problem of a pin joint system subjected to vertical load that acts at point B.Since the pin joint system cannot allow x or y movement there should be reactions at A and C which are resolved into their horizontal and vertical components.For determining their value the moment about the point C and A are taken to zero ,This is where I got stuck,

I cite the step in the book

ƩMc=0 => FAx*(a+b)-P*c
ƩMa=0 => P*c +FCx*(a+b)

What happened to the y components of the reactions at A and C.Why FCy and FAy are not taken,Is that because the force applied is vertical ?.I am self studying so I cannot clarify this with someone.I know this is elemantary but pls help me..

 

[Travis_King]

Take the equation you've got there for the moment about (c). How would a vertical force at (a) apply a moment about (c)? To find a moment you take a force and multiply it by a distance, what is that distance in the case of Fay about point (c)?

 

[jayanth nivas]

What I'm about ask is very basic.But I don't understand one thing.In the image the thread starter has shown,the points A and C are connected through B so if the load applied at B tries to push it down will the point C remain stationary because of the reaction offered by X component of A ?.If the points A and C are not collinear,will the Y component also offer resistance ? .Please explain me how with an example ?

And again please remember I'm learning the basics and I just wanted to learn this properly.Sorry if I'm asking something very basic

And thanks in advance.

 

[Travis_King]

Those circles at the A,B, and C locations generally denote "pinned" or "fixed" points. In problems like this, this means that any forces on the system will create reactionary forces, but the location of the pins will not move.

 

[caldweab]

Moment is a force times the perpendicular distance from the force to the point of rotation. There's no perpendicular distance for those two reactant forces, therefore no moment is created by them.