Solving a Pulley Problem with Unknown Variables

[jprg]

Hi,

I would like to solve this problem.
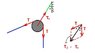
Pulley is attached to the green rope that is 2' long.
The weight is 1 unit.
a and b are unknown.
The green rope's point of attachment is 20' higher than that of the blue rope.
The distance between two walls is 20'.
I would like to solve this for the forces in the green rope and the angle the green rope is making with the wall.
I am not sure how to proceed.

Thanks.

 

[jprg]

I can write a computer program and use numerical approximation for this. But I would really like to solve this analytically so as to understand the mechanics of it.

By the way, the pulley diameter can be disregarded.

Do I need to get into calculus to solve this?

 

[hikaru1221]

No, calculus is unnecessary
Since total force on the pulley = 0, the sum of 2 tensions due to the blue rope must be in the same direction of the green rope (assume that friction is negligible). Denote x the angle needed, then the angle between the 2 sections of the blue rope is 2x.
We have: tanx = 1/(b/a+1) and tan2x = a/b, so: \frac{1}{tan2x}+1 =\frac{1}{tanx}
Moreover: tan2x=\frac{2tanx}{1-tan^2x}
From here, you may solve for x. Then the tension in the green rope can be easily found.

 

[jprg]

Thanks,

Can you clarify how you got tanx = 1/(b/a+1)

 

[hikaru1221]

Oops, sorry, I was wrong It should be tanx = a/(b+1). My mistake led me to think that the lengths were redundant.
By the way, what's dimension of a and b? At first I thought you used them to illustrate the ratios. But if you write b+1, "1" here should mean 1 meter or 1 cm, or so. With the lengths, I think it's solvable.

 

[jprg]

a and b just serve to denote force components. Their units are the same as the weight.
Since the weight is 1 unit acting straight down, and the vertical (downward) component on the blue rope's first section is denoted as b, then the green rope must counteract these too forces and have an upward vertical component equal to b+1. (b plus one unit).

Thanks.

 

[jprg]

It still doesn't make sense to me, as the calculations do not take the actual dimensional layout into consideration. But the forces and angles will change as the points of attachment or the distance between the walls change.

 

[hikaru1221]

Let's do it all over.

Denote T tension in the blue rope. Because the weight is at rest: T = W = 1 (unit of force).
As the pulley is at rest as well, we have: To = 2Tcosx = 2cosx.

Denote L the length of the left section of the blue rope. We have:
_ For the distance between the walls: 20 = 2sinx + Lsin2x
_ For the distance between the attachment positions: 20 = 2cosx + Lcos2x
Technically we can solve the 2 above equations for L and x. Then plug x to the first equation for To. But I'm too lazy to work it out Try to give it a shot

This way is easier I think, as we don't have to deal with a and b to find To.