Solving a Stationary Block on a Frictionless Wedge

[postfan]

Homework Statement

This is a 2 part question.

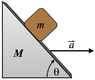
A block of mass m rests on a frictionless wedge that has an inclination of theta and mass M.
a) Find the acceleration of the wedge M to the right such that the block m remains stationary relative to the wedge.
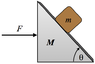
c) You now find out that a force of magnitude F was exerted (say, by somebody's hand) on the wedge as shown in the picture below. What is the magnitude F for which the block m remains stationary relative to the wedge? Use m, M, g, and theta.

Homework Equations

F=ma

The Attempt at a Solution

I drew a FBD but I can't fathom how acceleration in the horizontal will cause a block not to move in the vertical.

 

[Doc Al]

I drew a FBD but I can't fathom how acceleration in the horizontal will cause a block not to move in the vertical.

What force does the wedge exert on the block? How is that affected by the acceleration?

Do a FBD of the block.

 

[postfan]

The force is the normal force which is m*g*cos(theta) but I don't get how the acceleration affects it.

 

[Doc Al]

The force is the normal force which is m*g*cos(theta) but I don't get how the acceleration affects it.

Yes, the force is the normal force. But no, the normal force does not equal m*g*cos(theta) when the wedge is accelerating. (It does when the wedge is fixed.) The greater the acceleration, the harder the wedge presses against the block.

Just call the normal force "N" and apply Newton's laws to the block for vertical and horizontal components.

 

[postfan]

Is the normal force m*(g+a)*cos(theta)?

 

[haruspex]

Is the normal force m*(g+a)*cos(theta)?

That would look right if g and a were in the same direction, but they're not. Stop guessing: resolve forces and apply ƩF=ma in the vertical and horizontal directions in the usual way. What equations do you get?

 

[postfan]

In the vertical I get mg-mg*cos(theta)=ma a=g-g*cos(theta).
In the horizontal I get m*g*sin(theta)=m*a*sin(theta) a=g.

Is that right?

 

[Doc Al]

In the vertical I get mg-mg*cos(theta)=ma a=g-g*cos(theta).
In the horizontal I get m*g*sin(theta)=m*a*sin(theta) a=g.

Is that right?

Again, just call the normal force "N" (or any symbol of your choice). Rewrite those equations.

What must be the acceleration in the vertical direction if the block is not to slide down the wedge?

 

[postfan]

In the vertical I get mg-N=ma a=(mg-N)/m.
In the horizontal I get m*g*sin(theta)=m*a*sin(theta) a=g.

Is that right?

 

[haruspex]

In the vertical I get mg-N=ma a=(mg-N)/m.
In the horizontal I get m*g*sin(theta)=m*a*sin(theta) a=g.

Is that right?

No. First, let's get the set of forces right.
1. List the forces, giving their directions.
2. Write out the horizontal and vertical components of each force.
Then, and only then, should you try to write out the equations.

 

[postfan]

Iin the vertical you have the normal force . In the horizontal you have gravity and the force pushing the block (to have acceleration you need a force) Is that right?

 

[haruspex]

Iin the vertical you have the normal force .

A normal force means a force that is normal to (i.e. at right angles to) the surface. The surface is not horizontal, so the normal force is not vertical.

In the horizontal you have gravity

Last time I checked, gravity acts vertically.

and the force pushing the block (to have acceleration you need a force) Is that right?

Yes, F is horizontal.

 

[Doc Al]

In the horizontal you have gravity and the force pushing the block (to have acceleration you need a force) Is that right?

Careful. The force pushing the block is the normal force. Only two forces act on the block.

 

[postfan]

So in the vertical you have gravity and in the horizontal you have the force that is pushing the block. Is that right?

 

[HallsofIvy]

NO. That's what Doc Al has been trying to get you to see. gravity is vertical but the normal force, due to the wedge, is NOT horizontal. It is normal to the surface of the wedge. Separate it into normal and horizontal forces.

 

[postfan]

Ok so the the normal force is N*cos(alpha) and the horizontal force is N*sin(alpha). Is that right?

 

[Doc Al]

Ok so the the normal force is N*cos(alpha) and the horizontal force is N*sin(alpha). Is that right?

Let me restate what I think you're trying to say:

The normal force is N. The vertical component of that force is N*cos(theta); the horizontal component is N*sin(theta).

Good. Keep going.

 

[postfan]

Ok so from N2L the equations are N*sin(theta)=ma (x-axis) and N*cos(theta)-mg=0. Is that right?

 

[Doc Al]

Ok so from N2L the equations are N*sin(theta)=ma (x-axis) and N*cos(theta)-mg=0. Is that right?

Yes, that's right.

 

[postfan]

Ok so then the acceleration is (N*sin(theta))/m and the force is ((M+m)(N*sin(theta)))/m. Is that right?

 

[haruspex]

Ok so then the acceleration is (N*sin(theta))/m and the force is ((M+m)(N*sin(theta)))/m. Is that right?

Yes. Now use the vertical force equation to substitute for N.

 

[postfan]

Ok, so N=mg/cos(theta) , hence a=mg/cos(theta)*sin(theta))/m which = g*tan(theta) and the force=(M+m)*g*tan(alpha). Is that right?

 

[Doc Al]

When you solve for the acceleration, do not express it in terms of the unknown normal force.

 

[postfan]

I did not express it in terms of the normal force.

 

[Doc Al]

I did not express it in terms of the normal force.

Ah, OK.

Ok, so N=mg/cos(theta) , hence a=mg/cos(theta)*sin(theta))/m which = g*tan(theta) and the force=(M+m)*g*tan(alpha). Is that right?

Yes, that's correct now.

 

[postfan]

Cool! Thanks for all your help!