Jeroen Staps
- 36
- 0
Homework Statement
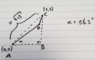
I need to solve a system of two equations for T and θ algebraic and with all the other parameters known.
φ is equal to:
Homework Equations
The relevant equations are the two equations left of * in the image below
The Attempt at a Solution
I tried Gauss elimination but I could not solve it further.
Now my question is if it is even possible to solve this algebraic to find T and θ.