Solving a Truss Reaction Problem: Find Reactions & Moment

[Deimos0239]

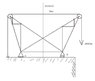
I have a little bit of an issue. I am trying to find the reactions on this truss. I know there are x and y at the first and y at the 2nd on the truss. But when I create my moment, do it take the 2500 lb into effect for the rope across the top and side as well? or do i omit those?

My thought would be a Y force of 2500 in the +Y Direction on the left, a +x force of 2500 at the top and a -Y force of 2500 on the right? Is that correct?

The only reason I ask is when I compute the moment at point a using the numbers I have, my Y reaction at A and B are the same and HUGE (over 10k) and my X component at A is 2500.

(Sorry the pic isn't that great. I don't have a scanner to show the actual problem but this is pretty close.)

 

[pongo38]

What you must be clear about is the object boundaries for which you wish to make an equilibrium statement. If you cut the structure at B, you rightly say that you replace the cut with a By force. At A the cut gives you an Ax and an Ay, as you have said. If you cut the horizontal rope, you must replace the cut with appropriate forces. In this case, there is little point because the forces are equal and opposite. But if you cut the vertical rope to the left of A, What is the magnitude and direction of the force you must replace the cut with?. Again the answer is two equal and opposite forces, one acting on the ground (the foundation), and one acting on your superstructure. Armed with that conclusion, you have enough information to sole the problem.

 

[Deimos0239]

Thanks for that information. I just wasn't sure when taking my torque (moment) around A if I should be including a force for the top rope or not..including that will change my numbers by roughly 3700 lbs...