whatdoido
- 48
- 2
Hi!
I cannot get rid of a mass and having some confusion about this whole problem.
1. Homework Statement
A car's wheelbase is 300 cm and its center of gravity horizontal distance from rear axle is 120 cm and its distance from the ground is 75 cm. Wheels and ground's coefficient of friction is 0,50. Specify maximum acceleration on a flat road if the car is rear wheel drive. With what solution this acceleration could be improved?
##x=120 cm=1,2 m##
##\mu=0,50##
##a=300 cm=3,0 m##
##b=75 cm=0,75 m##
##M=J\alpha##
##M=Fr##
J=\frac{1}{2}mr^2
\sum M=0
I drew an illustration about the problem:
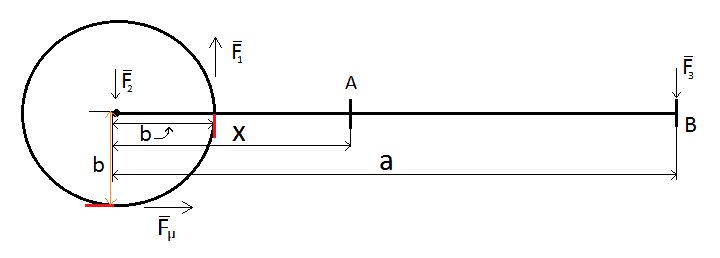
A is the center of gravity. I understand that the wheel creates a torque ##F_1b## when ##F_\mu\mu=F_1##. ##F_3a## is the torque that keeps the car's front down in relation to wheel. As far as I can see, I can try solving the acceleration with torques ##F_1b## and ##F_3a## in relation to the wheel(s) but obviously ##F_2## is the force that keeps car's rear down and cannot be ignored. I can solve car's proportional masses in relation to A with torques ##F_1x## and ##F_3(a-x)## but I don't know how that helps. So first step would be to know in what relation I should try solving torques. Also how to solve acceleration without knowing wheel's mass.
I cannot get rid of a mass and having some confusion about this whole problem.
1. Homework Statement
A car's wheelbase is 300 cm and its center of gravity horizontal distance from rear axle is 120 cm and its distance from the ground is 75 cm. Wheels and ground's coefficient of friction is 0,50. Specify maximum acceleration on a flat road if the car is rear wheel drive. With what solution this acceleration could be improved?
##x=120 cm=1,2 m##
##\mu=0,50##
##a=300 cm=3,0 m##
##b=75 cm=0,75 m##
Homework Equations
##M=J\alpha##
##M=Fr##
J=\frac{1}{2}mr^2
\sum M=0
The Attempt at a Solution
I drew an illustration about the problem:
A is the center of gravity. I understand that the wheel creates a torque ##F_1b## when ##F_\mu\mu=F_1##. ##F_3a## is the torque that keeps the car's front down in relation to wheel. As far as I can see, I can try solving the acceleration with torques ##F_1b## and ##F_3a## in relation to the wheel(s) but obviously ##F_2## is the force that keeps car's rear down and cannot be ignored. I can solve car's proportional masses in relation to A with torques ##F_1x## and ##F_3(a-x)## but I don't know how that helps. So first step would be to know in what relation I should try solving torques. Also how to solve acceleration without knowing wheel's mass.