davidmigl
- 7
- 0
Homework Statement
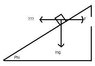
See the figure. This is part of a larger problem involving electromagnetism. I understand the electromagnetism but am having trouble with the basic mechanics!
I have a block of mass M on a frictionless incline at angle phi. There is a magnetic force acting horizontally on the block. I need to find the component of the normal force that balances this out.
The Attempt at a Solution
The component of the normal force parallel to the incline is mg*cos(Pi/2-phi)=mgsin(phi). The angle between this component is phi. Therefore, the horizontal component should be mgsin(phi)cos(phi).
However, my book says this should be mgtan(phi). I do not know how they got that. Perhaps setting the component of the magnetic force parallel to the incline equal to the component of the normal force parallel to the incline we get Fcos(phi)=mgsin(phi) so F=mgtan(phi). But if I try to find the component of the normal force in the opposite direction of the magnetic force, I get F=mgsin(phi)cos(phi). What gives?