Solving Circuit Problems with Permanent Rules: Charges, Currents & More

[libelec]

I have these two circuits with permanent rule:
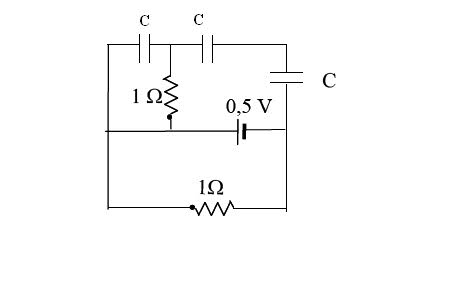
a)

b)

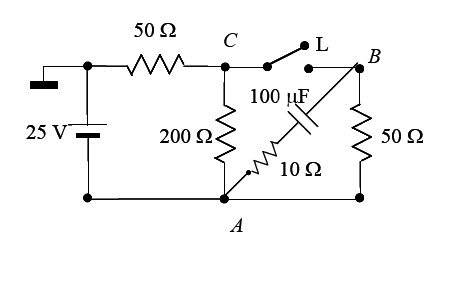
I'm asked to find:
For a): the charges of each capacitor (C = 1 $$\mu$$F)and the currents in each resistance.

For b): the currents in each branch with the L switch on and off, the difference of potential between A and C, A and B and C and B with the L switch on and off. The power given by the battery with L on and off and finally the charge of the capacitor with the switch on

The Attempt at a Solution

Here's my problem: I believe that, after a capacitor is charged, current doesn't flow through the branch that it's in, since after it's charged, it adquires the diference of potential of the battery (between its plaques) and therefore current shouldn't flow there. Is this correct?

Now, in each problem I have questions:

For a): Does each capacitor have the same difference of potential between its plaques, that of the battery (0,5V)? Is it OK to say that current isn't flowing through the 1 ohm resistance because it's connected to a branch that has a capacitor in it, and then current wouldn't be able to "escape" there?

For b): If the switch is off, is the equivalent circuit that square formed by the battery, the 50 ohm resistance and the 100 ohm resistance? Or does current somehow pass through the capacitor's branch (this relates to my original question).

Then, when the switch is on, should I consider each subdivision created by the diagonal branch in the second "square" for the Kirchhoff's Circuits Rule, or should I assume there's no current going through that branch (because the capacitor is charged?) and therefore I consider the whole square as the circuit?

Thanks.

 

[Delphi51]

Your thinking is right in every respect, except that remark about the potential being 0.5 V across each capacitor in (a): the two C's in series will each get half the 0.5 V, and the third one at upper left gets no voltage at all because of your argument that there is effectively infinite resistance across the charged capacitors, isolating that 3rd one from the negative end of the battery.

Yes in (b), you have infinite resistance in the diagonal loop so you can ignore it.

 

[libelec]

Ohhh... you're right, the 3rd one has no way to get to the negative terminal.

Well, thank your very much. I was worried I was making every calculation wrong because of a false assumption.

 

[libelec]

I tried to go back to a), to see what you meant with that the capacitor in the upper left gets no voltage because the infinite resistance of the other two.

If that was true, shouldn't the capacitor to its right also not get any voltage, because of the infinite resistance of the third capacitor? Why is that one the one that gets no voltage?

 

[libelec]

Did anybody understand what I meant?

 

[willem2]

The reason that the top left capacitor gets no voltage, is because it is in parallel with an 1 ohm resistance, and the current through this resistance is zero, so the voltage across it is also 0.
(ohms law)
No current can flow through the resistance, because one end of it is only connected to 2 capacitors and no current can flow through a capacitor after the steady state is reached.

 

[libelec]

What I mean is that the current through the resistance couldn't have been zero all along: otherwise, the other 2 capacitors couldn't have been charged at all, since there would be no way to connect the second capacitor with the positive terminal?

 

[libelec]

I mean, if we consider that at the beginning the capacitors were uncharged, then there's current flowing through the capacitor in the upper left corner, right?

 

[Delphi51]

That's a good point, libelec. But after the two Cs in series charge up to the full 0.5 V, it is as if that branch no longer exists (infinite resistance) and then the 1 ohm resistor will drain away the current in the upper right C. It would be interesting to calculate its charge as a function of time, but it is definitely zero once the steady state is reached.