Solving Differential Equation numerically

[aaaa202]

Homework Statement

I am supposed to write a script that can solve the Schrödinger equation on a nonuniform grid.

Homework Equations

Finite element approximation to the second derivative as in:
https://www.physicsforums.com/threads/nonuniform-finite-element-method.857334/#post-5382329

The Attempt at a Solution

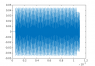
I have defined a grid x = [x1,x2,x3,...,x4] with nonuniform spacing and a potential V(x). Specifically the nonuniform spacing is such that the first 10 points have a spacing of 10^-10 and the others have 10^-9.
I have then solved the Schrödinger equation by finding eigenvectors of:
H = -ħ²/2m D + V

The problem is that these have some kind of weird oscillatory behaviour, which stems from the discontinuity in the distance between the grid points. Do anyone have an idea what I could be doing wrong?

 

[Simon Bridge]

How did you construct D?

 

[aaaa202]

Sorry that was not clear. I used the expression from my previous thread (second post):
https://www.physicsforums.com/threads/nonuniform-finite-element-method.857334/#post-5382329

 

[aaaa202]

I think if you use an approximation for the second derivative based on a nonuniform mesh, will this create some problems for the eigenvalue equation? Is it still valid that the eigenfunctions of the second derivative is just the eigenvectors of the matrix that represents it?