Solving Equilibrium of Glass Cylinder w/ Coil Wrapped Around It

[RichardEpic]

Homework Statement

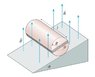
A glass cylinder of radius R, length l, and density \rho has a 10-turn coil of wire wrapped lengthwise, as seen in the figure . The cylinder is placed on a ramp tilted at angle \theta with the edge of the coil parallel to the ramp. A uniform magnetic field of strength B points upward.

For what loop current I will the cylinder rest on the ramp in static equilibrium? Assume that static friction is large enough to keep the cylinder from simply sliding down the ramp without rotating.
Express your answer in terms of the variables R, l, \rho, \theta, B, and appropriate constants.

Homework Equations

Force of gravity = mgSin(θ)

ρ = m / volume

volume = l*2∏R^2
l = length of the cylinder

B of coil = μIN/l
l = length of the solenoid

Force on a current = ILxB = ILBsin(θ)
L = length of the wire

The Attempt at a Solution

I attempted to solve this equation by solving for the mass from the density equation given above: m = ρl2∏R^2

so: Fg = gρl2∏R^2 * sin(θ)

then, I set this equal to the Force of magnetism on a current...

gρl2∏R^2 * sin(θ) = ILBsin(θ)

sin(θ)'s cancel...the l's also apparently cancel...giving me:

(gρl2∏R^2)/B = I

The homework website says that all I'm missing is an incorrect multiplier. How would I factor in torque for this problem? I believe that may be the solution, unless it has something to do with the glass cylinder and the coil wrapped around it, or perhaps there's something specific to a magnetic field acting on a solenoid...Help would be greatly appreciated!

 

[Joechieftw]

Your answer should have been I = g*rho*pi*R^2/(20B). This is due to the 2 sides affected by the magnetic force with 10 coils each making B=20IlB. This is to help anyone reading this archive and unfortunately not OP.