Saladsamurai
- 3,009
- 7
[SOLVED] FBD troubles
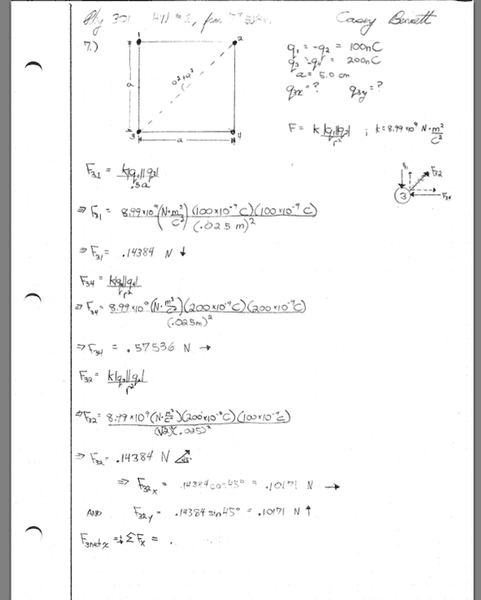
I am looking at 3-15 (with diagram). I am having trouble since there is no angle given.
I have so far -F+F_{ax}+F_{cx}=0 and in y direction F_{ay}=F{cy}.
Since the y components are equal, the springs have equal unstretched lengths, can I assume that the angle they make with the horizontal must be 45^\circ?
Or that since the vertical distance between the B and A must be 3 meters?
Or is this not the way to be looking at it?
Thanks,
Casey
Homework Statement
I am looking at 3-15 (with diagram). I am having trouble since there is no angle given.
I have so far -F+F_{ax}+F_{cx}=0 and in y direction F_{ay}=F{cy}.
Since the y components are equal, the springs have equal unstretched lengths, can I assume that the angle they make with the horizontal must be 45^\circ?
Or that since the vertical distance between the B and A must be 3 meters?
Or is this not the way to be looking at it?
Thanks,
Casey