Solving for Acceleration and String Forces on Incline with Two Masses

[stunner5000pt]

Tension Problem Please help!

Ok so i got this question

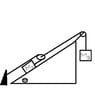
Look at the attached diagram
Althoughin the diagram i drew it doesn't look like it , Mass 1 on the incline is heavier than Mass 2 and the accleration is to the left.

The ramp is frictionless and the strings and pulleys are assumed to be massless
Find the acceleration on m2 and the string forces.

Now normally i wouldn't have trouble iwht something like this but that extra pulley throws me off

normally i'd think for the sum of the forces on mass 1

M_{1}a = M_{1} g Sin \theta - T
and
M_{2}a = T - M_{2} g

this however does not yield the answer after i plugged in Mass 1 = 0.4kg, Mass 2 = 0.2kg, and Theta = 30 degrees.

COuld you perhaps point out where my mistake lies and point me in the right direction. How does that left pulley influence that motion.

For the left pulley considering the mass and pulley and the wall alone

M_{1} g - T = M_{1} a and
T = reaction force of the wall??

Am i going off on a tangent, is this totally necessary for finding the acceleration on M2??

 

[MathStudent]

There are two distinct ropes in this scenario. Each rope has its own tension call it T1 and T2. Realize that the tension of the ropes is the same throught the entire length of the rope (since this is an ideal situation).

Your mistake comes from assuming that the tension on M2 is the same as the tension on M1.. but they are two distinct ropes.

Set up FBD's for M1 and M2 keeping in mind that T1 does not necessarily equal T2.

hint: the acceleration of that pulley equals the acceleration of M2

edit: oops forgot the pulleys were massless so the FBD for the pulley doesn't help, but the rest still stands

 

[Doc Al]

acceleration constraint

normally i'd think for the sum of the forces on mass 1

M_{1}a = M_{1} g Sin \theta - T
and
M_{2}a = T - M_{2} g

Since the masses are connected by ropes and a pulley, their accelerations are related. You assume that they are equal. Rethink that assumption.

Hint: If M_1 slides a distance x down the ramp, how far does the pulley (and thus M_2) slide down?

Edit: That's not your only mistake, as MathStudent points out: The ropes have different tensions.

 

[stunner5000pt]

hmm.. ok

so according to what mathstudent says then it would look something like this for the mass 1

M_{1} a_{1} = M_{1}g Sin \theta - T_{1}
but what is T1?

So since the pulley is massless then the two tensions are equal, should they be because if the pulley had a mass

M_{p} = M_{p} g Sin \theta + 2T_{1} - T_{2}
Something is wrong here isn't it ??

 

[Doc Al]

so according to what mathstudent says then it would look something like this for the mass 1

M_{1} a_{1} = M_{1}g Sin \theta - T_{1}
but what is T1?

It's an unknown which you will solve for, just like T2 and acceleration.

So since the pulley is massless then the two tensions are equal, should they be because if the pulley had a mass

M_{p} = M_{p} g Sin \theta + T_{1} - T_{2}
Something is wrong here isn't it ??

Yes, something is wrong: (1) the mass of the pulley is zero; (2) there are three rope segments exerting force on the pulley. (The tensions are not equal; but the net force on the pulley is zero.)

 

[stunner5000pt]

It's an unknown which you will solve for, just like T2 and acceleration.


Yes, something is wrong: (1) the mass of the pulley is zero; (2) there are three rope segments exerting force on the pulley. (The tensions are not equal; but the net force on the pulley is zero.)

I put a 2 in front of the T1 term for the rope does that make the difference??

 

[Doc Al]

I put a 2 in front of the T1 term for the rope does that make the difference??

Of course.

 

[stunner5000pt]

Of course.

So the 2 is correct?? Becuase the pulley feels 2 tensions in teh same direction due to the mass looping around it ?/

So then taht gives me

M_{1} a_{1} = M_{1} g Sin \theta - T_{1}
M_{2} a_{2} = T_{2} - M_{2} g
2T_{1} = T_{2}

But the solution for a1 and a2 is still impossible

 

[Doc Al]

So the 2 is correct?? Becuase the pulley feels 2 tensions in teh same direction due to the mass looping around it ?/

Yes, the 2 is correct. Picture an imaginary box enclosing the massless pulley: You'll see three ropes sticking out. Each rope exerts its tension on whatever is in the box. Since one rope loops around the pulley, it pulls twice. \Sigma F = 2T_1 - T_2 = m_{pulley}a = 0. So: T_2 = 2T_1.

 

[Doc Al]

So then taht gives me

M_{1} a_{1} = M_{1} g Sin \theta - T_{1}
M_{2} a_{2} = T_{2} - M_{2} g
2T_{1} = T_{2}

But the solution for a1 and a2 is still impossible

You give up too easily!

Follow my advice in post #3 and figure out the relationship between a1 and a2. (And be sure to use a consistent sign convention.)

 

[stunner5000pt]

i'm still here aren't i!

anyway i was just thinking of what you posted last : if mass 1 moxed x metres down the ramp how far down will the pulley move and I'm ... baffled

i can certainly find the relationship between a1 and a2 as follows
a_{1} = g Sin\theta - \frac{2M_{2}g}{M_{1}} - \frac{2M_{2}a_{2}}{M_{1}}

but if the mass 1 moved x down the ramp then ... the pulley would move half as much (just a guess there, I am not sure) please help

thank you

 

[Doc Al]

but if the mass 1 moved x down the ramp then ... the pulley would move half as much (just a guess there, I am not sure) please help

Exactly! So what does that tell you about how the two accelerations relate to each other?

Note: Guessing is OK to start. But don't stop there. Convince yourself that it's true by drawing the picture at two different points. (Or just play with a piece of string until you can visualize it.)

 

[stunner5000pt]

I see how that happens because the pulley will feel twice a tension force from the left and half as much on teh right so it will accelerate 1/2 as much as the mass 1 does because of the tension forces. SO then as a result of this happening

d = v t , v = at , d = at^2
for mass 1

x = a_{1} t^2
for the puller
\frac{x}{2} = a_{2} t^2

equating these two gets 2a_{2} = a_{1}

so then i sub this into the earlier expression
a_{1} = g Sin\theta - \frac{2M_{2}g}{M_{1}} - \frac{2M_{2}a_{2}}{M_{1}}

and i get 2a_{2} = \frac{g}{2} - g - a_{2}
which yields a2 = -g/6 and the answer is the back of the book is g/9??
is there something else with the acceleration tht i have not accounted for ??

 

[Curious3141]

but if the mass 1 moved x down the ramp then ... the pulley would move half as much (just a guess there, I am not sure) please help

thank you

You're right on the money there. This might make it clearer :

x_1 = 2x_2 where the subscripts refer to mass 1 and 2 respectively.

Differentiating twice with respect to time,

\ddot{x_1} = 2\ddot{x_2}

Does that tell you enough about the relationship of the accelerations ?

 

[Curious3141]

I see how that happens because the pulley will feel twice a tension force from the left and half as much on teh right so it will accelerate 1/2 as much as the mass 1 does because of the tension forces. SO then as a result of this happening

d = v t , v = at , d = at^2
for mass 1

x = a_{1} t^2
for the puller
\frac{x}{2} = a_{2} t^2

equating these two gets 2a_{2} = a_{1}

so then i sub this into the earlier expression
a_{1} = g Sin\theta - \frac{2M_{2}g}{M_{1}} - \frac{2M_{2}a_{2}}{M_{1}}

and i get 2a_{2} = \frac{g}{2} - g - a_{2}
which yields a2 = -g/6 and the answer is the back of the book is g/9??
is there something else with the acceleration tht i have not accounted for ??

I managed to get the book answer. Let us see your force equations. There should be two equations with two unknowns, the tension in the string attached to mass 2 and the acceleration of mass 2.

 

[stunner5000pt]

here are the force equations
for mass 1 on the left on the ramp
M_{1} a_{1} = M_{1} g Sin \theta - T_{1}

for the mass 2 on on the right
M_{2} a_{2} = T_{2} - M_{2} g

and the relationships between tension and accelerations
2T_{1} = T_{2}
a_{1} = 2a_{2}

 

[stunner5000pt]

finally got a2

i thank you for all the help you have given me really appreciate it