Haru Yo Koi
- 5
- 0
Thank you!
A very frustrating problem involving physics, and I finally decided to create an account and ask. And I typed up my problem, equations and all. But as I typed a certain equation, I suddenly wondered why I had cos in one place and sin in another. That was a mistake, and after fixing it, the answer turned up correct!
(Because I don't feel like losing my hard-typed stuff, it is saved below, or at least the beginning of it. There didn't seem a point in adding to it.)
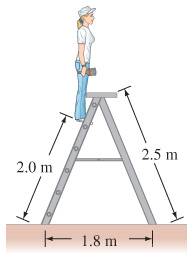
A 60.0-kg person stands 2.0 m from the bottom of the stepladder shown in the figure above. The horizontal rod is halfway up the ladder.
Find the tension in the horizontal rod, the normal forces on each side of the ladder, and the angle/direction of the force one side of the ladder exerts on the other.
Sum of torque = 0. Sum of forces in each direction = 0.
I'm trying to look at each side of the ladder separately.
The left seems to have four forces: A normal force F_{N} which points straight up, a tension force F_{T} which points straight rightwards, a F_{p} which points straight downwards, and a F_{0} which points upwards to the left at an angle \alpha from the horizontal.
The right side seems to be the same, except that [tex/]F_{0}points downwards \alpha from the horizontal and the normal force is F_{n}.<br /> <br /> Now some equations can be found.<br /> F_{0}sin(\alpha)=F_{n}<br /> F_{0}cos(\alpha)=F_{T}<br /> F_{N} + F_{0}sin(\alpha) = F_{p}<br /> (1/2)F_{t}sin(\theta) = F_{n}cos(\theta)<br /> (1/5)F_{p}cos(\theta)+(1/2)<br /> <br /> At this point I realized that what was on the right, which I had down as F_N(cos theta) should actually have been F_N(sin theta).
A very frustrating problem involving physics, and I finally decided to create an account and ask. And I typed up my problem, equations and all. But as I typed a certain equation, I suddenly wondered why I had cos in one place and sin in another. That was a mistake, and after fixing it, the answer turned up correct!
(Because I don't feel like losing my hard-typed stuff, it is saved below, or at least the beginning of it. There didn't seem a point in adding to it.)
Homework Statement
A 60.0-kg person stands 2.0 m from the bottom of the stepladder shown in the figure above. The horizontal rod is halfway up the ladder.
Find the tension in the horizontal rod, the normal forces on each side of the ladder, and the angle/direction of the force one side of the ladder exerts on the other.
Homework Equations
Sum of torque = 0. Sum of forces in each direction = 0.
The Attempt at a Solution
I'm trying to look at each side of the ladder separately.
The left seems to have four forces: A normal force F_{N} which points straight up, a tension force F_{T} which points straight rightwards, a F_{p} which points straight downwards, and a F_{0} which points upwards to the left at an angle \alpha from the horizontal.
The right side seems to be the same, except that [tex/]F_{0}points downwards \alpha from the horizontal and the normal force is F_{n}.<br /> <br /> Now some equations can be found.<br /> F_{0}sin(\alpha)=F_{n}<br /> F_{0}cos(\alpha)=F_{T}<br /> F_{N} + F_{0}sin(\alpha) = F_{p}<br /> (1/2)F_{t}sin(\theta) = F_{n}cos(\theta)<br /> (1/5)F_{p}cos(\theta)+(1/2)<br /> <br /> At this point I realized that what was on the right, which I had down as F_N(cos theta) should actually have been F_N(sin theta).