pka
- 11
- 0
Hello there! I'm new to this forum and not quite sure if this question has been asked before. I've posted a link to the picture of the circuit I am trying to solve for. The circuit is rather simple but I cannot get it. =/ I need to find the voltage across the capacitor. I need to figure out the correct technique in order to do this because I have tried a few different ways and they do not give me the correct answer. I'm more concerned with how to do problems like these (multiple resistors, capacitors and inductors) because I seem to be doing something wrong and...I'm becoming more confused. This is what I've done:
I've tried Kirchoff's circuit laws and this is what I've come up with:
Vs = VR1 + VC1 and VC1 = VL + VR2 + VR3
I solved for the impedance in the inductor (ZL) and for the impedance in the capacitor (ZC). I get ZC = -j and ZL = j10.
I figured that I could use the voltage divider rule to solve for the voltage across the first resistor (VR1) which would then be:
VR1 = Vs*[ (ZR1) / (ZR1 + ZL + ZC + ZR2 + ZR3) ]
This gives me 16.3 - j2.44
Solving for the voltage across the capacitor I get VC1 = Vs - VR1.
This then gives me 83.7 + j2.44
This isn't the correct answer and I'm pretty sure not the correct way to approach this problem, lol. I don't think I've done the voltage divider rule correctly. In fact, I'm a little confused as to using the voltage divider rule. Can I still use it even though this circuit is made up of series and parallel components?
I have not tried doing a mesh current analysis just yet, but that to me seems to confuse me and take me in a circle just as much as the voltage analysis does.
Any help anyone can offer would be greatly appreciated! And many thanks in advance.Circuit:
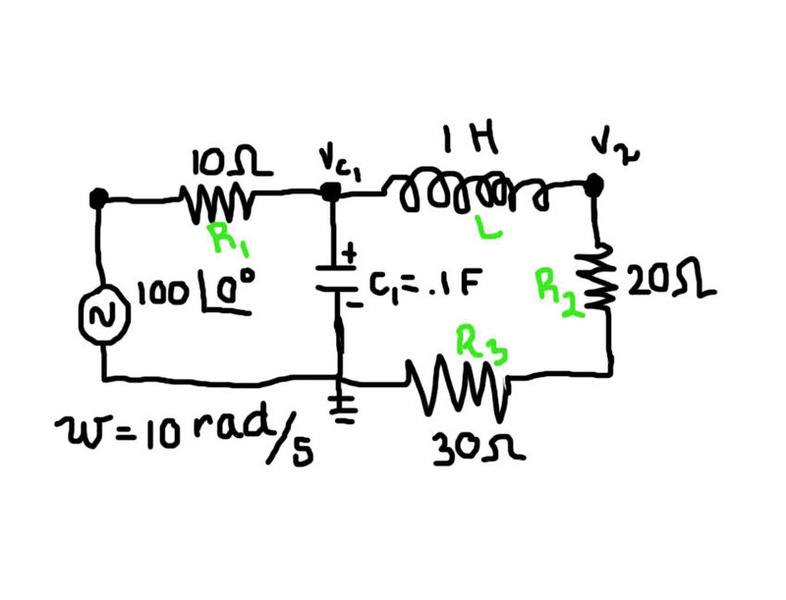
I've tried Kirchoff's circuit laws and this is what I've come up with:
Vs = VR1 + VC1 and VC1 = VL + VR2 + VR3
I solved for the impedance in the inductor (ZL) and for the impedance in the capacitor (ZC). I get ZC = -j and ZL = j10.
I figured that I could use the voltage divider rule to solve for the voltage across the first resistor (VR1) which would then be:
VR1 = Vs*[ (ZR1) / (ZR1 + ZL + ZC + ZR2 + ZR3) ]
This gives me 16.3 - j2.44
Solving for the voltage across the capacitor I get VC1 = Vs - VR1.
This then gives me 83.7 + j2.44
This isn't the correct answer and I'm pretty sure not the correct way to approach this problem, lol. I don't think I've done the voltage divider rule correctly. In fact, I'm a little confused as to using the voltage divider rule. Can I still use it even though this circuit is made up of series and parallel components?
I have not tried doing a mesh current analysis just yet, but that to me seems to confuse me and take me in a circle just as much as the voltage analysis does.
Any help anyone can offer would be greatly appreciated! And many thanks in advance.Circuit:
Last edited: