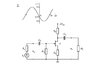
amsi
- 7
- 0
Okay I feel really stupid for getting wrong omega for such a trivial problem.
1. Homework Statement
Find the function of e(t) = A* sin(wt + fi)
A = 0.9 V
at t = 0 e(t) = -0.35, and therefore:
-0.35 = 0.9 * sin (w*0 + fi) / * arcsin
arcsin(-7/18)= fi
fi = -22.89 degrees = -0.4 rad
at t = 26 us , A = 0 V, and therefore:
0 = 0.9 * sin (w*26u -0.4 ) / *arcsin
0 = w*26 u - 0.4
w = 0.4/26 * 10 ^- 6
w = 15384 rad / s which is not correct
1. Homework Statement
Find the function of e(t) = A* sin(wt + fi)
Homework Equations
The Attempt at a Solution
A = 0.9 V
at t = 0 e(t) = -0.35, and therefore:
-0.35 = 0.9 * sin (w*0 + fi) / * arcsin
arcsin(-7/18)= fi
fi = -22.89 degrees = -0.4 rad
at t = 26 us , A = 0 V, and therefore:
0 = 0.9 * sin (w*26u -0.4 ) / *arcsin
0 = w*26 u - 0.4
w = 0.4/26 * 10 ^- 6
w = 15384 rad / s which is not correct