Solving Homework Problem on \alpha = 37, m1 = 10 kg

[asi123]

Homework Statement

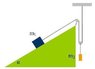
\alpha = 37, m1 = 10 kg
Also attachment.

Homework Equations

The Attempt at a Solution

ok, the first question is to find m2 when the system is in rest and the second one is to find the acceleration when m1 = m2.
I found 3 equations:
n1 = m1 * g * cos(\alpha )
m1 * g * sin(\alpha ) = T2
T1 + T2 = m2 * g
I need another one I think...

Could it be that T1 = T2?
And as for the second one, how can I find the equations between the accelerations? (there is always one...)

10x in advance.

 

[Dick]

Yes, the tensions of lengths of rope connected by frictionless pulleys have the same tension. But in your Newton's law F=ma equations, I only see F parts, I don't see any ma parts. You don't even have an acceleration to solve for...

 

[asi123]

Yes, the tensions of lengths of rope connected by frictionless pulleys have the same tension. But in your Newton's law F=ma equations, I only see F parts, I don't see any ma parts. You don't even have an acceleration to solve for...

Yeah, because the first set of questions is for acceleration = 0 (the system is in rest).
Here are the equations for the second question:

T - m1 * g * sin(\alpha) = m1 * a1
m2 * g - 2 * T = m2 * a2

I need the accelerations equation and I don't know how to come up with that...

10x.

 

[Dick]

Good point, a=0 for the first part. Sorry, I missed that. But for the second part there is another relation between a1 and a2. Consider the length of rope going through each part of the pulley system. Total length of rope is constant. One acceleration is twice the other. Which is which?

 

[asi123]

Good point, a=0 for the first part. Sorry, I missed that. But for the second part there is another relation between a1 and a2. Consider the length of rope going through each part of the pulley system. Total length of rope is constant. One acceleration is twice the other. Which is which?

I have no idea...
I would like to think m2 is faster cause the g force is stronger with him But I'm not sure.
I didn't get you, how can I see it through the length of the rope?

10x.

 

[Dick]

If m1 descends 1 meter down the ramp, how much does m2 rise? You can tell just by looking at the length of the rope. The total length of the rope on m2's side of the pulley decreases by 1 meter.