Solving Kirchoff's Rules for R1=10 Ohms, R2=15 Ohms, R3=5 Ohms

[wazzup]

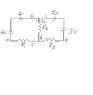
Q) Given R1=10 Ohms, R2=15 Ohms, R3=5 Ohms, find the current going through each resistor in this pathway in the attached circuit diagram.

My solution is as follows.. i'd appreciate it if you guys could verify if its correct or not:

I2=I1+I3-------------------------Equation 1

Starting from a and going through loop agdf:

-E1+I2R2+I1R1=0
15I2+10I1=6 -----------------Equation 2

Starting from k and going through loop kmdl:

-I3R3-I2R2+E2=0
-5I3-15I2=-3--------------------Equation 3

Plugging Equation 1 into Equation 2

15I2+10(I2-I3)=6
25I2-10I3=6--------------------Equation 4

Adding Equation 3 and Equation 4

25I2 - 10I3= 6
-15I2 - 5I3=-3

By multiplying equation 4 by 2 and then subtracting both, I get:

55I2=12
I2= .218A

Plugging this value of I2 into Equation 4:

25I2-10I3=6
25(.218) - 10I3=6
-10I3=.55
I3= -0.055A

Plugging I2 and I3 into Equation 1

I2=I1+I3
I1=I2-I3
I1= (.218A)-(-0.055A) = .273A

Therefore, I1= 0.273A
I2= 0.218A
I3= -0.055A

Thanks much.

 

[Gladi8or2]

Your equations seem correct to me. I didn't solve them, but that shouldn't be a problem.

 

[wazzup]

I got this answer wrong on a test for some reason. Could anyone confirm that they got the same answers ( in case I messed up on the algebra,etc )?

Thanks

 

[topsquark]

Looks good to me. And well organized to boot!

-Dan

 

[nrqed]

I got this answer wrong on a test for some reason. Could anyone confirm that they got the same answers ( in case I messed up on the algebra,etc )?

Thanks

You know, you can always check your algebra by simply plugging back your values of current in the initial equations. If they work (within a certain precision) then you know you did not mess up the algebra.
The only other way to go wrong is in writing the initial equations in the first place.

Patrick

 

[wazzup]

Thanks much guys.. Appreciate it :)