ApeXaviour
- 34
- 0
Right, I was looking over some past exam papers from these science-maths scholarship exams I was looking to do. It's all revision for me but it's been a while. Anyway, skimming over the double integration questions. Now if I recall correctly it's a fairly simple process, integrate the inner bit, then the outer et voila right? Ok you got a bit more with oddly shaped areas (type I and II etc) and whatnot but it's still pretty straightforward.
I hit a bump, embarrassingly just with the mechanics of integrating itself, I just couldn't damn remember what to do when the question came up like this.
To elaborate, I'd come across this question:
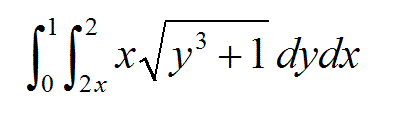
Now, if I'm doing this correctly I initially ignore the outer nested bits and concentrate on this:
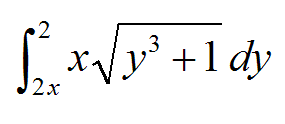
Wtf do I do with that? I put it through mathematica and it comes up with some "null" argument jive.
Skimmed numerous times through all relevant sections of my calculus book (by Anton) to no avail..
Looked at the previous year's question and sure enough there was one just like it:
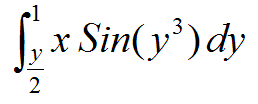
With no such example in my obviously inferior recommended text I'm left to ask for help.
Cheers
-Dec
I hit a bump, embarrassingly just with the mechanics of integrating itself, I just couldn't damn remember what to do when the question came up like this.
To elaborate, I'd come across this question:
Now, if I'm doing this correctly I initially ignore the outer nested bits and concentrate on this:
Wtf do I do with that? I put it through mathematica and it comes up with some "null" argument jive.
Skimmed numerous times through all relevant sections of my calculus book (by Anton) to no avail..
Looked at the previous year's question and sure enough there was one just like it:
With no such example in my obviously inferior recommended text I'm left to ask for help.
Cheers
-Dec
