Solving Newton's Laws: Mass m Reaches Table in 1.08s

[assaftolko]

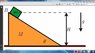
a mass of m=6 kg is free to move without friction on a body with a mass of M=18 kg at an angle of theta=32 deg. M is placed on a friction free table. At the moment t=0 m is released from rest from the top of M at an height of H=4m .

At what moment does m reach to the table?

I'm uploading the question and my solution, which is t=1.54 s, while the correct answer should be t=1.08 s. I'd like to know what I did wrong...

 

[Simon Bridge]

Compare:
https://www.physicsforums.com/showthread.php?t=66006
Without knowing your reasoning it is difficult to know how to describe the mistake.
The comparison should help you figure it out.

 

[assaftolko]

Compare:
https://www.physicsforums.com/showthread.php?t=66006
Without knowing your reasoning it is difficult to know how to describe the mistake.
The comparison should help you figure it out.

What do you mean "my reasoning"? I can't see why I got the wrong answer and I uploaded a detailed solution... Obviouslly I have a mistake along the way...

 

[voko]

What do you mean "my reasoning"? I can't see why I got the wrong answer and I uploaded a detailed solution... Obviouslly I have a mistake along the way...

At the end of your attempt, you get the acceleration of m w.r.t. M. However, M itself is accelerated. It is not an inertial frame of reference and I do not see you have made any attempt to account for that.

Nor do I think it is required. I think all you need is conservation of energy and horizontal momentum.

 

[assaftolko]

At the end of your attempt, you get the acceleration of m w.r.t. M. However, M itself is accelerated. It is not an inertial frame of reference and I do not see you have made any attempt to account for that.

Nor do I think it is required. I think all you need is conservation of energy and horizontal momentum.

But I did account for that, I got the acceleration of m w.r.t M using the Delambre force on m. And relative to M, m passed the distanc L did it not?

 

[voko]

You may have tried, indeed. Problem is, I find it difficult to distinguish a_M from a_m in that picture. Could you post the equations here to avoid any misunderstanding?

 

[assaftolko]

You may have tried, indeed. Problem is, I find it difficult to distinguish a_M from a_m in that picture. Could you post the equations here to avoid any misunderstanding?

The first 2 equations are on M and in the second one it's aM. and it says: "aM is the accerleration of M relative to the ground!".

The next equation is the Fy equation on m, and it says:

N+m*aM*sin(theta)-mgcos(theta)=0 where m*aM*sin(theta) is the Delambre force in the y-axis direction of m's coordinate system (drawn at the right side of the picture)

After that linr I simply put N=(M*aM)/sin(theta) and after some calculations you get an expression for aM.

Afterwards the Fx equation for m is written and it says:

m*aM*cos(theta)+mgsin(theta)=m*am where m*aM*cos (theta) is the Delambre force in the x-axis direction of m's coordinate system. After I put the expression I got for aM you can get an expression for am, which is the acceleration of m relative to M.

Hope this helps

 

[voko]

I have followed your derivation and I cannot spot any problem with it.

Moreover, if your expression for a_m is simplified, it can be seen that in the limit of infinite M it results in a_m = g sin \theta, as it should be for the immovable wedge, and in the limit of \theta → \pi / 2 it results in a_m = g, again as it should be. So I have strong reasons to believe that your solution is correct.