Solving Scalar Product Problem: Find Perpendicular Distance

[pavadrin]

Hey,
Today I was given a problem to solve in class and was told to complete it for homework. This problem is as follows:

The line y=mx + c has a gradient m and cuts the y-axis at (0,c). Thus we can write the parametric vector equation of the line as:

r = cj +\lambda (i + mj)

Using this fact show that that the perpendicular distance from point A(x_1 , y_1) to y = mx + c is:

\mid(\frac{mx_{1} - y_{1} + c}{\sqrt{m^2 + 1}})\mid

If y = mx + c is instead written as ax + by + d = 0 show that the perpendicular distance of point A(x_1 , y_1) to as ax + by + d = 0 is given by:

\mid(\frac{ax_{1} - by_{1} + d}{\sqrt{a^2 + b^2}})\mid

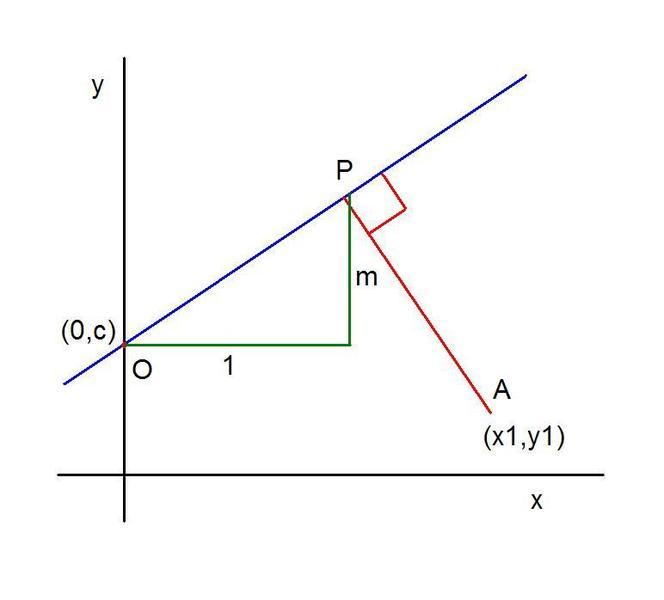
This diagram which I drew to help me may help:

______________________​

I have tried solving this problem by using vectors:

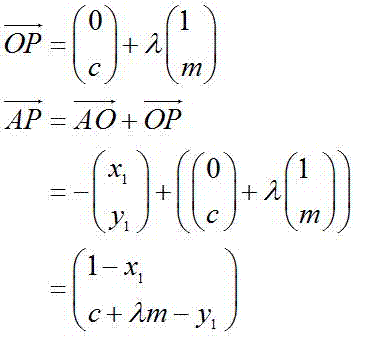
and I know that the dot product of ( x_1 , y_1 ) and y = mx + c is equal to zero but from there onwards I am not sure on how to approach this problem. All help is appreciated,
thanks, Pavadrin

 

[e(ho0n3]

First, you need to find a vector perpendicular to the line y = mx + c. Call this vector u. Let v be the vector that points to A. Then for some n, nu + v = r. The magnitude of nu is the perpendicular distance from the point A to the line y = mx + c.