Solving Stone Falling on Earth: Coriolis & Centrifugal Forces

[Karol]

Homework Statement

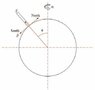
A stone falls from a tower on some latitude on earth, like in the picture. how far from the base and in which direction will it fall.
We take into account the Coriolis force, but neglect the centrifugal acceleration since it's small.
The problem is solved in a book, but i want to know if and how we take in consideration the Earth's radius if i want to take into account the centrifugal acceleration also.

Homework Equations

The "F" notation is for the fixed coordinate system and "R" for the rotating one.
$$\vec{a}_R=\vec{a}_F-2\vec{\omega}\times\vec{V}_R-\vec{\omega}\times\left(\vec{\omega}\times \vec{r} \right)$$

The Attempt at a Solution

$$\vec{r}=x\hat{x}+y\hat{y}+z\hat{z}$$
According to this notating we don't have the radius of the earth.
Also the teacher said that we search for the centrifugal force on a rotating object that is itself in a rotating frame, so, according to the relative acceleration formulas:
$$\vec{a}_1=\omega^2\left(\vec{R}_e+\vec{r}_1 \right)$$
$$\vec{a}_{2}=\omega^2\left(\vec{R}_e+\vec{r}_2 \right)$$
$$\vec{a}_{12}=\vec{a}_2-\vec{a}_1=\omega^2\left(\vec{r}_2-\vec{r}_1 \right)$$
And the Earth's radius is limited.
But i don't think so, since the centrifugal force on the stone is according to the Earth's radius.
And, tell me if i am wrong, the centrifugal (and also coriolis) forces are dependent, according to this calculation, on the choice of the rotating system's base, the nearer to the center of the Earth the stronger the forces, but the force on the stone is one.
Shouldn't i have chosen both, the rotating and the fixed systems to share the same origin? is it possible to solve such questions with different origins?
I don't know what is wrong, i cannot write those 3 equations as tex, can anyone tell me why?

 

[Karol]

The last sentence should be erased, i succeeded to write the equations in Tex