M.D.G
- 18
- 0
I’m pretty stumped by this, maybe I am just making a stupid mistake but if somebody could clarify it would be much appreciated.
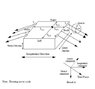
The system I am looking at is something like the one below, with 4 straps of each side. Their locations relative to the center of gravity along the lateral direction is not symmetric but back to front they are symmetric. Each strap has a lateral, longitudinal and vertical component. I need to determine the tension in each of the straps when resisting an acceleration of 3g in the longitudinal direction.
The problem I am have is I only have 2 equations,
A force balance, i.e. T1 + T2 + T3 + T4 = mass*3*g
And a moment blance, i.e. T1*y1+T2*y2 = T3*y3 + T4*y4
Where T1 … T4 are the tensions in the longitudinal direction, and y1 .. y4 are the distances from the CG along the lateral axis.
Am I missing something?
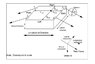
Edit: To clarify I drew a bird's eye view of the problem. The black arrows represent tie down lines, the red arrow represent a force acting through the center of mass due to an acceleration of 3g's
The system I am looking at is something like the one below, with 4 straps of each side. Their locations relative to the center of gravity along the lateral direction is not symmetric but back to front they are symmetric. Each strap has a lateral, longitudinal and vertical component. I need to determine the tension in each of the straps when resisting an acceleration of 3g in the longitudinal direction.
The problem I am have is I only have 2 equations,
A force balance, i.e. T1 + T2 + T3 + T4 = mass*3*g
And a moment blance, i.e. T1*y1+T2*y2 = T3*y3 + T4*y4
Where T1 … T4 are the tensions in the longitudinal direction, and y1 .. y4 are the distances from the CG along the lateral axis.
Am I missing something?
Edit: To clarify I drew a bird's eye view of the problem. The black arrows represent tie down lines, the red arrow represent a force acting through the center of mass due to an acceleration of 3g's
Attachments
Last edited: