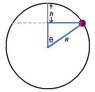
SUMMARY
The discussion focuses on solving the Olympic Ring Puzzle, which involves calculating the maximum mass of a large circular ring supporting two identical beads, each with a mass of 30 kg. Participants suggest using conservation of energy to relate angular speed and height, and emphasize the importance of understanding the forces acting on the system, including gravitational force and normal force. The key equations discussed include mgh = 1/2mv² and mgcosθ + Fn = mv²/R, which are essential for determining the conditions under which the tension in the rope becomes zero.
PREREQUISITES
- Understanding of conservation of energy principles
- Familiarity with centripetal force and normal force concepts
- Knowledge of angular motion and its equations
- Ability to analyze forces in a dynamic system
NEXT STEPS
- Study the derivation of centripetal acceleration in circular motion
- Learn how to apply conservation of momentum in dynamic systems
- Explore the relationship between angular displacement and height in circular motion
- Investigate the effects of varying mass and angle on tension in a system
USEFUL FOR
Physics students, mechanical engineers, and anyone interested in dynamics and force analysis in circular motion will benefit from this discussion.