Solving the Olympic Ring Puzzle: Calculate Max Mass

[SuperHero]

Homework Statement

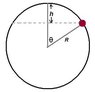
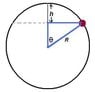
This is the diagram http://s1302.beta.photobucket.com/user/Rameel17/media/dd_zps43d04d44.png.html

A single large circular Olympic ring hangs freely at the lower end of a strong flexible ring which is firmly supported at the other end. Two identical beads each has a mass of 30 kg are free to slide without friction around the ring. The ring passes through the hole in the beads. The two beads are released from rest at the very top as shown of the ring. At least once during their fall to the bottom the tension in the rope is zero. Calculate the maximum mass of the king in kg.

The Attempt at a Solution

I am not sure where to being for this one.

 

[tiny-tim]

Welcome to PF!

Hi SuperHero! Welcome to PF!

You could use conservation of energy to find the relationship between angular speed and height.

And you could consider what happens to the centre of mass.

 

[SuperHero]

Hi SuperHero! Welcome to PF!

You could use conservation of energy to find the relationship between angular speed and height.

And you could consider what happens to the centre of mass.

Okay so do you mean like this

mgh = 1/2mvo^2
(30kg)(9.8m/s^2)h=1/2(30kg)(v^2)
(30kg)(9.8m/s^2)h/1/2(30kg) = v^2

Fc = ma
Fc = m (vc^2/R)

right? :D

 

[tiny-tim]

Hi SuperHero!

(try using the X² and X₂ buttons just above the Reply box )

mgh = 1/2mvo^2
(30kg)(9.8m/s^2)h=1/2(30kg)(v^2)
(30kg)(9.8m/s^2)h/1/2(30kg) = v^2

there are two velocities, that of the beads, and that of the large ring

Fc = ma

that's not correct … ma equals the total force (including the weight)

anyway, more useful would be:

total change in momentum = sum of all external forces​

(and I'm off to bed :zzz:)

 

[SuperHero]

total change in momentum = sum of all external forces​

What do you mean by this?
I am really confused..
So this is what is given to us.
V1 of bead 1 = 0m/s
V1 of bead 2 = 0m/s
bead 1 mass = 30 kg
bead 2 mass = 30 kg
T= 0
Mass of ring = ?

Now what do i do?
Are you trying to tell me that i should use total conservation of momentum? or?

 

[haruspex]

You need to find the position of the masses at which the tension is minimised. Suppose this is when the lines from the ring's centre to the masses are at angle theta to the vertical. Use conservation of energy to find the speeds at that point. Then you can work out the normal force from ring to masses, and from that the tension in the string.

 

[tiny-tim]

Hi SuperHero!

I think I've misunderstood the set-up …

my computer wouldn't show me your picture, and i thought the large ring was moving …

please ignore what i previously wrote

Okay so do you mean like this

mgh = 1/2mvo^2
(30kg)(9.8m/s^2)h=1/2(30kg)(v^2)
(30kg)(9.8m/s^2)h/1/2(30kg) = v^2

yes

(except you could have canceled m on both sides, and it might be better to use θ as your variable, rather than v)

find the equation for the normal force, as haruspex suggests​

 

[SuperHero]

Hi SuperHero!

I think I've misunderstood the set-up …

my computer wouldn't show me your picture, and i thought the large ring was moving …

please ignore what i previously wrote


yes

(except you could have canceled m on both sides, and it might be better to use θ as your variable, rather than v)

find the equation for the normal force, as haruspex suggests​

Okay so like this

mgh = 1/2mvo^2
(30kg)(9.8m/s^2)h=1/2(30kg)(v^2)
(30kg)(9.8m/s^2)h/1/2(30kg) = v^2

but i am so lost. I do not understand how i can use the above equation to find the v^2 if we don't even know the height.

 

[tiny-tim]

Hi SuperHero! Happy new year!

… I do not understand how i can use the above equation to find the v^2 if we don't even know the height.

That's an equation relating h and v.

So you can find the centripetal acceleration at a general height h.

What is the relation between the tension in the string and the centripetal acceleration (at height h)?​

 

[SuperHero]

Hi SuperHero! Happy new year!


That's an equation relating h and v.

So you can find the centripetal acceleration at a general height h.

What is the relation between the tension in the string and the centripetal acceleration (at height h)?​

will they be point down?

 

[TSny]

In order to motivate why you should even bother with writing the conservation of energy equation or why you need to worry about centripetal acceleration, see if you can conceptualize what causes the big ring to be “lifted” upward so that the tension in the string can go slack. It must be some force acting on the ring. Can you describe all the forces acting on the big ring as the beads are sliding? Can you identify which of those forces is (are) responsible for lifting up the ring? The answer is not immediately obvious. But if you can see what it is, it will provide a motivation for what equations to write down and what to solve for.

(I hope I'm not side-tracking the thread. If so, just ignore this.)

 

[SuperHero]

In order to motivate why you should even bother with writing the conservation of energy equation or why you need to worry about centripetal acceleration, see if you can conceptualize what causes the big ring to be “lifted” upward so that the tension in the string can go slack. It must be some force acting on the ring. Can you describe all the forces acting on the big ring as the beads are sliding? Can you identify which of those forces is (are) responsible for lifting up the ring? The answer is not immediately obvious. But if you can see what it is, it will provide a motivation for what equations to write down and what to solve for.

(I hope I'm not side-tracking the thread. If so, just ignore this.)

Well some of the forces acting on the ring are force of gravity, the tension, and the normal force. The normal force is responsible for lifting up the ring. right?

 

[SuperHero]

OKay so i was doing a little research on this type of question, apparently there is a force known as the normal force that acts against the beads and the force of gravity changes into mgcosθ.
Furthermore they come up with this equation mgcosθ - N = mv^2/R then they have plugged this equation into the conservation of momentum equation which becomes
mg(2R) = 1/2mv^2 + mgR(1+cosθ)

 

[TSny]

Well some of the forces acting on the ring are force of gravity, the tension, and the normal force. The normal force is responsible for lifting up the ring. right?

Those aren't just some of the forces, those are all of the forces if you include the normal force from each bead. Good. And, yes, the normal forces from the beads are responsible for lifting up the ring. Or, more precisely, the vertical components of the normal forces on the ring are what lift the ring.

So, you're going to need to find an expression for the normal force that each bead exerts on the ring. The expression will depend on the position of the beads. The position of the beads are determined by θ, where θ is the angle between the vertical and a line drawn from the center of the ring to one of the beads

 

[SuperHero]

Those aren't just some of the forces, those are all of the forces if you include the normal force from each bead. Good. And, yes, the normal forces from the beads are responsible for lifting up the ring. Or, more precisely, the vertical components of the normal forces on the ring are what lift the ring.

So, you're going to need to find an expression for the normal force that each bead exerts on the ring. The expression will depend on the position of the beads. The position of the beads are determined by θ, where θ is the angle between the vertical and a line drawn from the center of the ring to one of the beads

so like this?

mgcosθ - Fn = m(v^2/R)

 

[TSny]

so like this?

mgcosθ - Fn = m(v^2/R)

This looks like the equation describing the forces on one of the beads, right? If so, then F_n here is the normal force on one of the beads. Just to make sure we're on track, how is that normal force related to the normal force acting on the ring?

 

[SuperHero]

This looks like the equation describing the forces on one of the beads, right? If so, then F_n here is the normal force on one of the beads. Just to make sure we're on track, how is that normal force related to the normal force acting on the ring?

well there are two beads.
if we add them together, then that would be the normal force pulling the ring right?

 

[TSny]

Yes, each bead exerts a normal force on the ring. So, there are two normal forces on the ring.

I just wanted to make sure that you see the relationship between the normal force that the ring exerts on a bead and the normal force that a bead exerts on the ring. These are "action-reaction" forces so they have the same magnitude but opposite directions. So, if you can find F_n acting on a bead, then the normal force acting on the ring will have the same magnitude but opposite direction.

For the total centripetal force acting on a bead, you wrote mgcosθ - F_n, with a minus sign for F_n. Doesn't that mean that you are considering the force F_n on the bead as acting outward (away from the center)? If so, then the force on the ring would be in the opposite direction, which would be inward toward the center of the ring. That is not going to lift the ring. (We assume θ<90^o)

As a bead begins to slide on the ring, the normal force on the bead is indeed outward. But, as the bead picks up more and more speed, it needs more and more centripetal force in order to travel in a circle. At some point (θ<90^o ), the normal force on the bead actually changes direction and points inward to help provide sufficient centripetal force on the bead. Then, the normal force on the ring is outward and tends to lift the ring. So, you want to be considering the case where the normal force on the bead is inward in the same direction as mgcosθ. So, your formula would be mgcosθ + F_n = mv²/R

 

[SuperHero]

ok so mgcosθ + Fn = mv2/R is my equation

so i would plug this into the conservation of energy formula

right?

 

[haruspex]

ok so mgcosθ + Fn = mv2/R is my equation

so i would plug this into the conservation of energy formula

right?

Yes, in the sense that you use the expression for v² that you obtained from conservation of energy.

 

[SuperHero]

Yes, in the sense that you use the expression for v² that you obtained from conservation of energy.

ok so like this
mgh = 1/2mvo^2
(30kg)(9.8m/s^2)h=1/2(30kg)(v^2)
(30kg)(9.8m/s^2)h/1/2(30kg) = v^2

mgcosθ + Fn = mv2/R

R(mgcosθ + Fn)/m = v^2

(30kg)(9.8m/s^2)(2R)/1/2(30kg) = R(mgcosθ + Fn)/m

 

[haruspex]

ok so like this
mgh = 1/2mvo^2
(30kg)(9.8m/s^2)h=1/2(30kg)(v^2)
(30kg)(9.8m/s^2)h/1/2(30kg) = v^2

We'll all find this much easier if you stick with symbols throughout the algebra, only plugging in numbers right at the end.

(30kg)(9.8m/s^2)(2R)/1/2(30kg) = R(mgcosθ + Fn)/m

No, you need the velocity when the line from centre of circle to bead is theta from the vertical. What is h there?

 

[SuperHero]

We'll all find this much easier if you stick with symbols throughout the algebra, only plugging in numbers right at the end.

No, you need the velocity when the line from centre of circle to bead is theta from the vertical. What is h there?

Umm would it be 2Rsinθ or?

 

[TSny]

Umm would it be 2Rsinθ or?

No. Consider the figure attached.

 

[SuperHero]

No. Consider the figure attached.

So wait. i have this equation for the 1 bead
mgcosθ + Fn = mv2/R

now what should i do?
You guys gave me the diagram.
But isn't the height the diameter of the circle?
Like i don't know?

 

[TSny]

So wait. i have this equation for the 1 bead
mgcosθ + Fn = mv2/R
now what should i do?

You're going to need an expression for the normal force and the above equation is a good start. You can rearrange it to solve for F_n. But that will express F_n in terms of two variables: θ and v. You can use the energy equation to help write F_n in terms of just the one variable θ. Once you've done that you can try to find the maximum value that the vertical component of F_n will have as the bead slides down. That will give you the maximum "lifting force" of one of the beads.

You guys gave me the diagram.
But isn't the height the diameter of the circle?

When you wrote mgh = (1/2)mv², what does "h" stand for? Yes, it's "height". But what height specifically?

The kinetic energy gained by the bead (from the point where it started to some point specified by θ) equals the magnitude of the loss of potential energy from the point where it started. That's what mgh = (1/2)mv² expresses. So, h (in mgh) must represent the vertical height that the bead has fallen from the point where it started to the point where the bead is at angle θ.

 

[SuperHero]

Yes that is what i was trying to do above and yes i understand what the h stands for now. But when i plug it into the conservation of energy formula, you said i would be able to find the Fn, but then what would i plug in or the h then?

 

[haruspex]

Yes that is what i was trying to do above and yes i understand what the h stands for now. But when i plug it into the conservation of energy formula, you said i would be able to find the Fn, but then what would i plug in or the h then?

Look at the diagram TSny kindly drew. How far has the bead descended when at angle theta above the centre? That's h.

 

[TSny]

Yes that is what i was trying to do above and yes i understand what the h stands for now. But when i plug it into the conservation of energy formula, you said i would be able to find the Fn, but then what would i plug in or the h then?

You have two equations to work with:

mgcosθ + F_n = mv²/R

mgh = (1/2)mv²

See if you can use the second equation to find an expression for mv² and then substitute that into the first equation. You can then solve for F_n to express F_n in terms of both θ and h. Finally you will be able to express h in terms of θ by geometry using the figure given earlier. That will give you the expression that you need for F_n in terms of just the variable θ.

 

[SuperHero]

so would it be Rcosθ = h right?