Solving the Pendulum Problem: Find d for a Complete Circle

[ek]

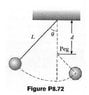
A pendulum, comprising a string length L and a small sphere, swings in the vertical plane. The string hits a peg located a distance d below the point of suspension. Show (A) that if the sphere is released from a height below that of the the peh, it will return to this height after striking the peg and (B) that if the pendulum is released from the horizontal position and is to swing in a complete circle centred on the peg, then the minimum value of d must be 3L/5.

These questions just kill me. There's always one on the assignment and it's always the one question I can't do.



Any help would be greatly appreciated.

 

[marlon]

Think of conservation of total energy : \frac{1}{2}mv^2 + mgh = constant

First try to determin this constant by looking at given boundary values, i mean like initial values for the velocity or height...then use this law to descirbe the motion. From the "peg" on, just look at the problem as a pendulum with a shorter string. You need to know something on the height or velocity just at the moment that the sphere is at the bottom of the trajectory...

These are some general clues...try to implement them...

good luck

regards
marlon

 

[Doc Al]

for part b

In addition to energy conservation, as marlon advised, realize that for part b there is a minimum speed at the top of the motion required to maintain some bit of tension in the string. Hint: consider centripetal acceleration and Newton's 2nd law.

 

[ek]

I'm still having problems with this question. Marlon, what does this constant represent?

Do I have to figure in that pendulum formula anywhere along the line or can it be done purely with energy considerations?

 

[marlon]

The constant is a general number. You have got to find the exact value by using some given values for the kinetic and potential energy...


marlon