Solving the SHM differential equation

[member 731016]

Homework Statement

Please see below

Relevant Equations

x(t) = Ae^(αt)

I am trying to solve this homogenous linear differential equation

.
Since it is linear, I can use the substitution

.
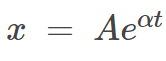Which gives,

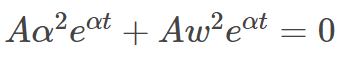(line 1)

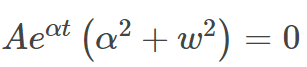(line 2)

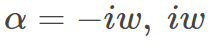(line 3)

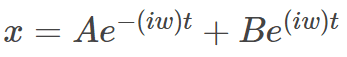(line 4)

(line 5)
Which according to Morin's equals,

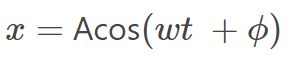(line 6)

However, could someone please show me steps how he got from line 5 to 6?

Also was is line 4 is it not:

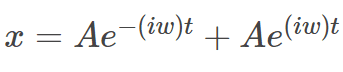? In other words, why dose B ≠ A?

Many thanks!

 

[kuruman]

All of the expressions below are general solutions of your equation

1. $x=C_1e^{i\omega t}+C_2e^{-i\omega t}$
2. $x=A\sin\omega t+B\cos\omega t$
3. $x=D\sin(\omega t+\phi)$

You can verify that this is so by substituting in your ODE. Note that each expression has two arbitrary constants that are determined by the initial conditions, usually the values of $x$ and $\frac{dx}{dt}$ at $t=0$ that are appropriate to a particular situation..

You are asking how to go from 5 to 6 which is essentially going from my item 2 to 3. It is more obvious to see how to go from 3 to 2. Once you see that, you can reverse the algebra, if you wish.

Using a well known trig identity for the sine of a sum of angles,
$$D\sin(\omega t+\phi)=D\cos\phi \sin\omega t+D\sin\phi \cos\omega t.$$ If you identify $$A\equiv D\cos\phi~~\text{and}~~B\equiv D\sin\phi,$$you have item 2 above.

 

[member 731016]

All of the expressions below are general solutions of your equation

1. $x=C_1e^{i\omega t}+C_2e^{-i\omega t}$
2. $x=A\sin\omega t+B\cos\omega t$
3. $x=D\sin(\omega t+\phi)$

You can verify that this is so by substituting in your ODE. Note that each expression has two arbitrary constants that are determined by the initial conditions, usually the values of $x$ and $\frac{dx}{dt}$ at $t=0$ that are appropriate to a particular situation..

You are asking how to go from 5 to 6 which is essentially going from my item 2 to 3. It is more obvious to see how to go from 3 to 2. Once you see that, you can reverse the algebra, if you wish.

Using a well known trig identity for the sine of a sum of angles,
$$D\sin(\omega t+\phi)=D\cos\phi \sin\omega t+D\sin\phi \cos\omega t.$$ If you identify $$A\equiv D\cos\phi~~\text{and}~~B\equiv D\sin\phi,$$you have item 2 above.

Thanks for your reply @kuruman ! Why don't you have and imaginary unit when going from line 1 to line 2? I though from Euler's identity it should be:

. However, are you assuming that the constant B accounts for that?

Many thanks!

 

[kuruman]

All arbitrary coefficients are, well, arbitrary which means they could be complex.

 

[member 731016]

Ok thank you @kuruman ! I guess that means we could have the coefficient without the imaginary unit, which is cool because even thought the answers look different, they are both correct.