- #1
gharrington44
- 9
- 0
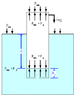
A hollow cylinder with closed ends is 300 mm in diameter, 450 mm high, has a mass
of 27 kg and has a small hole in the bottom. With its axial vertical, it is lowered
slowly into water, and then released. Calculate
a. The gauge pressure of the air inside it
b. The height to which the water will rise within it
c. The depth to which it will sink
Disregard the effect of the thickness of the cylinder wall but assume that it is uniform
and that the compression of the air inside is isothermal.
I already created an equation to find the pressure of the air inside the cylinder.
P = Patm +γ(h-h')
where h is the height of the column of the pressurized air in the cylinder and h' is the height of the cylinder that is protruding out of the water.
Using this I continued to make an equation for the forces on the cylinder. I figured the forces on the cylinder would be an upward buoyant force from the water, a downward weight, and a downward pressure force acting on the surface area of the cylinder. So my equilibrium equation would be...
Fb = W + PA where P is the air pressure that we said above so,
Aγ(H-h') = mg + [Patm + γ(h-h')]A once everything is simplified, we get...
h = H - [mg + APatm]/Aγ
Apparently this doesn't work because I get a negative value for h, and the height of the air column in the cylinder cannot be negative. My professor provided the calculated answers to these questions but the solutions are provided. someone please give me some insight
of 27 kg and has a small hole in the bottom. With its axial vertical, it is lowered
slowly into water, and then released. Calculate
a. The gauge pressure of the air inside it
b. The height to which the water will rise within it
c. The depth to which it will sink
Disregard the effect of the thickness of the cylinder wall but assume that it is uniform
and that the compression of the air inside is isothermal.
I already created an equation to find the pressure of the air inside the cylinder.
P = Patm +γ(h-h')
where h is the height of the column of the pressurized air in the cylinder and h' is the height of the cylinder that is protruding out of the water.
Using this I continued to make an equation for the forces on the cylinder. I figured the forces on the cylinder would be an upward buoyant force from the water, a downward weight, and a downward pressure force acting on the surface area of the cylinder. So my equilibrium equation would be...
Fb = W + PA where P is the air pressure that we said above so,
Aγ(H-h') = mg + [Patm + γ(h-h')]A once everything is simplified, we get...
h = H - [mg + APatm]/Aγ
Apparently this doesn't work because I get a negative value for h, and the height of the air column in the cylinder cannot be negative. My professor provided the calculated answers to these questions but the solutions are provided. someone please give me some insight