[Something descriptive here will yield more responses]

[tanzl]

Homework Statement

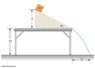
In the flgure below, the incline has mass M and is fastened to the stationary horizontal tabletop. The block of mass m is placed near the bottom of the incline and is released with a quick push that sets it sliding upward. It stops near the top of the incline, as shown in the flgure, and then slides down again, always without friction. Find the force that the tabletop exerts on the incline throughout this motion.

Homework Equations

The Attempt at a Solution

My answer is (M+m)g. But, it looks too simple to be correct.
Please clear my doubts.
1)Although there is a normal force of magnitude mg*cos(theta) that will eventually balance the weight of the mass m since the mass is not moving downward o upward.
2)The initial push on the mass m is not necessary to be considered in the calculation because the force supplied is not constant and so the only force acting on mass m which parallel to the incline is mg*sin(theta).

 

[dynamicsolo]

The picture hasn't come up yet, but your description points to something you need to consider. The normal force provided by the incline against the block is not vertical; thus, the "reaction force" of the block against the incline is not vertical. The table must in turn exert forces against the weight of the incline and block and this "reaction" force. Make a free-body diagram showing all the forces acting on the incline from both the block and the table. What must the forces from the table be in order that the net force on the incline comes to zero?