wislagrew
- 5
- 0
Hello,
I have two question regrading sound waves.
The first one:
The pressure P(x;t) at a point x at time t in a medium through which a harmonic wave is
travelling can be described by:
P(x,t) = Asin(wt -kx)
If the equation describes a pressure wave traveling in air, with amplitude 2 Pa and frequency 100 Hz,
find the instantaneous pressure at a distance 10 cm from the source at time 5s.
My solution(am I doing right?):
w=2pi*f
w=2pi*100Hz = 200pi rad/sec;
k=2pi/λ; v=f*λ; λ=343m/s /100 Hz = 3.43m and k=2pi/3.43 =1.83 rad/m;
Finally I have this:
P(x=0.1 ,t=5) = 2sin(200pi*5 -1.18*0.1) = -0.34.
The second question is here
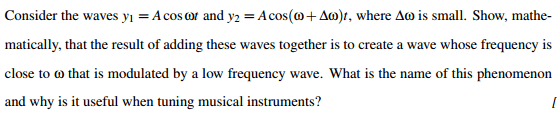
Hope you can help me to figure out the solutions.
Thanks
I have two question regrading sound waves.
The first one:
The pressure P(x;t) at a point x at time t in a medium through which a harmonic wave is
travelling can be described by:
P(x,t) = Asin(wt -kx)
If the equation describes a pressure wave traveling in air, with amplitude 2 Pa and frequency 100 Hz,
find the instantaneous pressure at a distance 10 cm from the source at time 5s.
My solution(am I doing right?):
w=2pi*f
w=2pi*100Hz = 200pi rad/sec;
k=2pi/λ; v=f*λ; λ=343m/s /100 Hz = 3.43m and k=2pi/3.43 =1.83 rad/m;
Finally I have this:
P(x=0.1 ,t=5) = 2sin(200pi*5 -1.18*0.1) = -0.34.
The second question is here
Hope you can help me to figure out the solutions.
Thanks