Sound waves - Detector and a moving wall

[Saitama]

Homework Statement

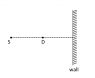
A sound source, detector and a movable wall are arranged as shown in the figure. In this arrangement detector is detecting the maximum intensity. If the speed of sound is 330 m/s in air and frequency of source is 600 Hz, then find the distance by which the wall should be moved away from the source, so that detector detects minimum intensity.

Homework Equations

The Attempt at a Solution

I don't quite understand the situation. Do the waves reflected by the wall ever reach the detector? I don't see how the reflected waves would reach the detector. (Can I assume that the waves get reflected the same way as a light ray would? )

Any help is appreciated. Thanks!

 

[ehild]

Have you experienced echo in your life? All waves can reflect...

ehild

 

[Saitama]

Have you experienced echo in your life? All waves can reflect...

ehild

Yes, I have experienced it but for that the reflected waves should reach the detector. But here they don't.

 

[ehild]

Why not? The reflected wave travels backwards.

ehild

 

[Saitama]

Why not? The reflected wave travels backwards.

ehild

So the sound waves don't reflect as the light rays would?

 

[ehild]

They reflect the same way, but here the incidence is normal. That sound source can be a loudspeaker, not a "point source"

 

[Saitama]

They reflect the same way, but here the incidence is normal. That sound source can be a loudspeaker, not a "point source"

Okay but how should I begin making the equations?

 

[ehild]

Think. How can the sound arrive by two different ways to the detector?

ehild

 

[Saitama]

Think. How can the sound arrive by two different ways to the detector?

ehild

By reflection and directly from the source.

 

[ehild]

And what is the path difference?

 

[Saitama]

And what is the path difference?

For constructive interference or maximum intensity, it is $n\lambda$ and for destructive interference or minimum intensity it is $\displaystyle \left(n+\frac{1}{2}\right)\lambda$ but I still have no idea what am I supposed to do with this.

 

[ehild]

What is the geometric path difference between the reflected wave and the directly arriving wave at the detector? And consider the phase change at the wall, too.


ehild

 

[Saitama]

What is the geometric path difference between the reflected wave and the directly arriving wave at the detector? And consider the phase change at the wall, too. ehild

There will be a phase change of $\pi$ which corresponds to a path difference of $\frac{\lambda}{2}$.
\Delta p=\left(d+x+\frac{\lambda}{2}\right)-(d-x)
\Delta p=2x+\frac{\lambda}{2}
Is this correct?

 

[ehild]

Yes.

 

[Curious3141]

What is the geometric path difference between the reflected wave and the directly arriving wave at the detector? And consider the phase change at the wall, too.


ehild

Will there be a phase change at the wall? It's of higher acoustic impedance than the air.

 

[Saitama]

Will there be a phase change at the wall? It's of higher acoustic impedance than the air.

I just checked my notes. It says that there will be no phase change when the wave is reflected from the rigid boundary.

Should I make the equations again?

 

[Curious3141]

I just checked my notes. It says that there will be no phase change when the wave is reflected from the rigid boundary.

Should I make the equations again?

Of course, if there's a change in your assumptions, there'll be a change in your equations.

 

[ehild]

I just checked my notes. It says that there will be no phase change when the wave is reflected from the rigid boundary.

Should I make the equations again?

Yes. Omit the Lambda/2.

 

[Saitama]

Of course, if there's a change in your assumptions, there'll be a change in your equations.

Since there is no phase change, for maximum intensity,
2x=n\lambda
For destructive interference
2x'=\left(n+\frac{1}{2}\right)\lambda
Change in distance between the detector and wall
\Delta x=x'-x=\frac{\lambda}{4}
\Delta x=0.125 m

Thanks a lot both of you, this is the right answer.

 

[Curious3141]

Since there is no phase change, for maximum intensity,
2x=n\lambda
For destructive interference
2x'=\left(n+\frac{1}{2}\right)\lambda
Change in distance between the detector and wall
\Delta x=x'-x=\frac{\lambda}{4}
\Delta x=0.125 m

Thanks a lot both of you, this is the right answer.

Isn't $\displaystyle \frac{\lambda}{4} = 0.1375m$?

$\displaystyle \lambda = \frac{v}{f} = \frac{330ms^{-1}}{600s^{-1}} = 0.55m$

 

[Saitama]

Isn't $\displaystyle \frac{\lambda}{4} = 0.1375m$?

$\displaystyle \lambda = \frac{v}{f} = \frac{330ms^{-1}}{600s^{-1}} = 0.55m$

Sorry about that, its 660 Hz in the question. That's a typo in the main post. :)

 

[Curious3141]

Sorry about that, its 660 Hz in the question. That's a typo in the main post. :)

Ah, OK.