Source free RL Circuit derivation

[jaus tail]

Hi,
I'm struggling with source-free RL Circuit derivation.

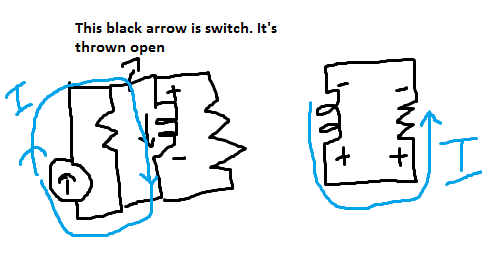
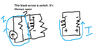
In the books in the right side diagram they've reversed polarity of inductor to get equation:
V_(r) = - V_(L)
But why?
I checked google and everywhere they had put inductor with positive sign upwards.

Here is what I think--
In left diagram, inductor is acting as a load, so the point where current enters is positive.
But in right diagram, inductor is a current source, so the point where the current leaves should be positive.
The resistance on right is load. So using KVL we get V_(r) = V_(L)

Where am I wrong? How to reach the equation--V_(r) = -V_(L)
V(r) is voltage across resistance on right side.
V(L) is voltage across inductor.

 

[tech99]

The LH circuit is a parallel circuit, so the resistors have no affect on the action of the inductor.
The inductor is like a flywheel; it is hard to get the current moving in it, so if the current is growing, after switch-on, then the inductor opposes the increase. So it is positive up in your circuit. But if the current is falling, as at switch-off, it tries to keep the current flowing, so is negative up in your circuit.
The resistors always oppose the flow of current so are always positive up in your LH circuit.

 

[jaus tail]

But if the current is reducing then in the right side diagram, current is flowing up in the resistor so shouldn't the lower terminal be positive and the upper one be negative as per sign conventions.

 

[donpacino]

I'm guessing the reason you are having trouble is notation. Either there is a diagram you are not showing us, or you drew the diagram wrong, or the question is terrible. Can you show us the actual book problem.

The voltage across the inductor and the resistor will be the equal they are two parallel components, unless you do something stupid like defining the voltages opposite each other. note: I'm not saying what you did was stupid, you actually pointed out the flaw in the logic.

What they likely are trying to portray is that with a positive value current source, when the switch is opened, current through the inductor will continue to flow, which will lead to a negative voltage, as the current flow will be going up through the resistor.

 

[Tom.G]

Where am I wrong?

You Aren't. In fact you are absolutely right!

 

[jaus tail]

I am studying from notes and I used this link
Link

How to get the equation iR + Ldi/dt = 0
Since in second diagram inductor is now like a source then using KVL we get source voltage = sum of voltage drops in circuit, so we get: Ldi/dt = iR
This is different from above equation.

 

[donpacino]

Since in second diagram inductor is now like a source then using KVL we get source voltage = sum of voltage drops in circuit, so we get: Ldi/dt = iR

forget about that acting like a source... It's acting like an inductor. You don't switch the polarity because you think its acting like a source.

If you INSIST on saying its acting like a source, then you have your Vr upside down. You had it correct in post 3.

 

[jaus tail]

I'm confused. Is the voltage polarity across inductor in right diagram correct in my drawing?
Should the equation be: V_L = V_R or V_L + V_R = 0
Link says it should be right one. I'm not able to understand how.

 

[jaus tail]

Is this correct polarity?
And then for RC circuit they've used:

Why is Ic flowing to the right? Ic should also flow toward the left. It's almost as if they've purposely used that direction of Ic just to reach the conclusion Ic + Ir = 0, whereas it should be Ir = Ic as both are in series.

 

[donpacino]

Why is Ic flowing to the right? Ic should also flow toward the left. It's almost as if they've purposely used that direction of Ic just to reach the conclusion Ic + Ir = 0, whereas it should be Ir = Ic as both are in series.

first off I am not sure where the capacitor example came from.

Second, this is something that beginners to electronics often mess up. It's something that took me a while to grasp. Direction like that does not matter, just use the notation that is simplest for you.

The fact of the matter is in that diagram IC is labeled in one direction, and Ir is labeled in the other. You correctly pointed out that IC=-IR, because it does.
the best way to attack these problems is define polarity, then if an answer comes up negative, that's fine. It is perfectly acceptable to say IR=5A and IC = -5A

 

[cnh1995]

Is this correct polarity?

For the inductor circuits, yes. In the RH diagram, the current direction should be reversed.
For the capacitor circuit, I agree with your reasoning about the current direction.

Consider an RL circuit excited with an independent voltage source V (left hand circuit in your post). Treat the voltages across the components (R and L) as voltage drops .
Write the KVL as,
Independent voltage= sum of all the voltage "drops" across the components.
So, the equation becomes
V=iR+Ldi/dt.

Now consider the RH circuit, which is source-free i.e. no independent source.
∴0=Ldi/dt+iR
∴V_L+V_R=0.
So, V_L= -V_R.

 

[jaus tail]

Now consider the RH circuit, which is source-free i.e. no independent source.
∴0=Ldi/dt+iR
∴V_L+V_R=0.
So, V_L= -V_R.

Shouldn't it be
0 = -Ldi/dt + iR... since now the inductor voltage will be positive at the lower end and negative at the upper end.

 

[cnh1995]

since now the inductor voltage will be positive at the lower end and negative at the upper end.

No, driving voltage is zero here. You should still consider the RHS terms to be voltage 'drops'. If you solve this equation, you'll get the correct expression for i(t).

If you use V_L=V_R,
you'll have Ldi/dt=iR, which doesn't give the correct expression for current.

With reference to a common terminal of R and L, it is correct that V_L=V_R. But while writing KVL, we take a 'KVL walk' around the loop and hence, we see a potential rise in the inductor and a potential drop in the resistor, both adding up to zero.
Hence, V_L+V_R=0 and V_L= -V_R. Here V_L and V_R are treated as voltage 'drops'. Since they have opposite signs, it is clear that one of them is now 'supplying' power.

 

[jaus tail]

This is what I'm struggling to understand. When the switch is opened(RH Diagram), there is current through the inductor. But this current comes from the magnetic energy stored in the inductor during switch was closed(LH Diagram).

So in LH Diagram, inductor acts as load as it is storing energy as magnetic field. But in RH Diagram the inductor loses this energy so shouldn't we follow KVL convention that
Sum of voltage source = sum of voltage drops
So Ldi/dt = iR.

maybe it's like
During storing energy di/dt is positive
while during releasing energy di/dt is negative so as it is Ldi/dt becomes negative so -Ldi/dt will be a positive value which is equal to iR which is positive as direction of current through R hasn't changed.

I understood. I assumed there to be a voltmeter connected across

So in first case let switch be closed so V source is acting. So voltmeters V_R and V_L will give positive values.

In second case voltmeter V_L will give me negative value as it is fall of current. Ldi/dt is negative.
Thus the formula: V_R + V_L = 0

This is assuming I haven't changed the terminals of voltmeters after the switch has moved.

 

[cnh1995]

Let VL1 be potential across inductor when it is storing energy and let VL2 be potential across inductor when it's releasing energy.
So in LH Diagram: V(source) = VR + VL1
In RH Diagram: VL2 = VR
And we have: VL2 = - VL1
And since VL1 = Ldi/dt
we have VR = VL2 = -VL1 = -Ldi/dt
So I get VR = -Ldi/dt

Yes, that's the math I was going to post. But here, you know that the inductor voltage changes polarity, before even solving for i(t).

But before solving this problem, even if you didn't know about the polarity change, you can still arrive at the correct result. Just put 0 in place of V_source in the green equation above.

 

[jaus tail]

Yes at first we have Vsource = V_R + V_L
= V_R + Ldi/dt
where di/dt is positive.

Now suppose source is short circuited so equation becomes:
0 = V_R + V_L as u said above
And this is electrically true because now di/dt is negative
so we have 0 = (a positive value) + (a negative value)