- #1
Dimani4
- 50
- 0
Hi people,
I have a question about the frame of references.
Let's have an example:
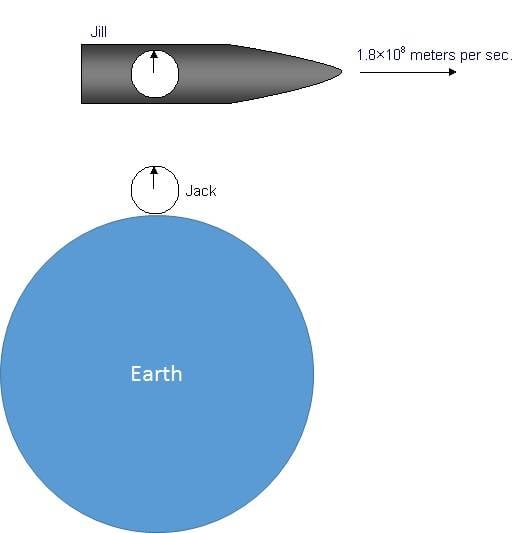
First case: Jill on rocket and Jack stationary on Earth. Jill moves relatives to Jack 0.6c (1.8*10^8m/s). The distance is 18*10^8m. At the zero time Jack and Jill synchronize their clocks. Then Jill starts to move. When Jill arrives 18*10^8 m Jack's clock shows 10sec but Jill's clock shows 8 sec. Here we can say Jill while she moves sees distance less than 18*10^8m in factor of 0.8 then for her she moves a distance of 18*10^8*0.8 then 18*10^8*0.8/1.8*10^8m/s=8ses as she sees at her clock. That's what happens from the point of Jack's view. Jack's clock shows 10sec while when he observes Jill's clock he sees 8sec.
2. Second case. Now let us see what happens from the point of view of Jill. As for her she doesn't know she's moving then for her Jack is moving (with Earth) and she's stationary. Now when Jill is stationary and Jack moves away from her with velocity of 0.6c. What time will be on Jill's and Jack's clock after the same distance as in the First case?
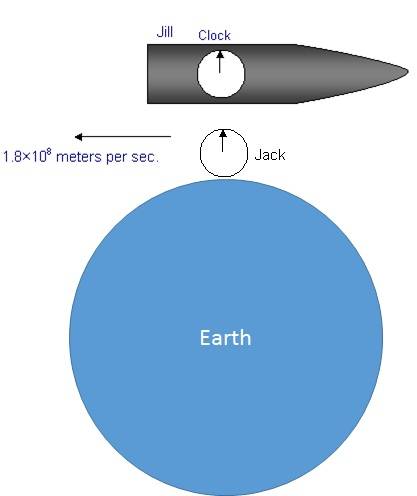
The clocks of them should show exactly the same time as was in the previous case. Isn't it? As for me now Jill's clock will show 10sec and Jack's 8 sec.
Thank you.
I have a question about the frame of references.
Let's have an example:
First case: Jill on rocket and Jack stationary on Earth. Jill moves relatives to Jack 0.6c (1.8*10^8m/s). The distance is 18*10^8m. At the zero time Jack and Jill synchronize their clocks. Then Jill starts to move. When Jill arrives 18*10^8 m Jack's clock shows 10sec but Jill's clock shows 8 sec. Here we can say Jill while she moves sees distance less than 18*10^8m in factor of 0.8 then for her she moves a distance of 18*10^8*0.8 then 18*10^8*0.8/1.8*10^8m/s=8ses as she sees at her clock. That's what happens from the point of Jack's view. Jack's clock shows 10sec while when he observes Jill's clock he sees 8sec.
2. Second case. Now let us see what happens from the point of view of Jill. As for her she doesn't know she's moving then for her Jack is moving (with Earth) and she's stationary. Now when Jill is stationary and Jack moves away from her with velocity of 0.6c. What time will be on Jill's and Jack's clock after the same distance as in the First case?
The clocks of them should show exactly the same time as was in the previous case. Isn't it? As for me now Jill's clock will show 10sec and Jack's 8 sec.
Thank you.

