Speed of Block at Top of Track: Solving Friction Problem

  • Thread starter Thread starter AdnamaLeigh
  • Start date Start date
  • Tags Tags
    Block Velocity
AI Thread Summary
The discussion focuses on calculating the speed of a block at the top of a vertical circular track, considering the effects of friction. The block, with a mass of 0.5 kg, is initially pushed against a spring and released, achieving a speed of 14 m/s at the bottom of the track. The user initially misapplied energy conservation principles by not correctly accounting for the negative work done by friction. The correct approach involves recognizing that the work done by friction reduces the total mechanical energy, leading to a lower speed at the top of the track. Clarification on the signs in the energy equation is essential for accurate calculations.
AdnamaLeigh
Messages
42
Reaction score
0
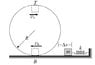
A block of mass .5kg is pushed against a horizontal spring of negligible mass, compressing the spring a distance of Δx (I solved for this and got .421m) as shown in the figure. The spring constant is 553N/m. When released, the block travels along a frictionless horizontal surface to point B, the bottom of the vertical circular track of radius .7m, and continues to move up the track. The speed of the block at the bottom of the track is 14m/s, and the block experiences an average frictional force of 6N while sliding up the track.
What is the speed of the block at the top of the track?
I know that normally the change in kinetic energy is equal to potential energy, but this is the not the case due to friction. This is the formula I used:
(6)(pi)(.7) - (1.4)(9.8)(.5) = .5(.5)v^2 - .5(.5)(14)^2
The 2nd half of the equation is equal to the change in kinetic energy. The 1.4 stuff is equal to the potential energy (m*g*h) But I'm really confused as what to do with the friction. I just multiplied the force of friction with half of the circumference.
I don't know how else to approach this, but I know it's wrong because my answer was 14.9m/s and the speed shouldn't be greater on top than bottom. This is frustrating. Thanks for any help.
 

Attachments

  • figure.jpg
    figure.jpg
    9.5 KB · Views: 422
Physics news on Phys.org
You're approach is OK, you are just messing up with signs. The change in energy (KE + PE) between bottom and top equals the work done by friction (which is negative).
 
Thread 'Variable mass system : water sprayed into a moving container'

Thread 'Variable mass system : water sprayed into a moving container'

Starting with the mass considerations #m(t)# is mass of water #M_{c}# mass of container and #M(t)# mass of total system $$M(t) = M_{C} + m(t)$$ $$\Rightarrow \frac{dM(t)}{dt} = \frac{dm(t)}{dt}$$ $$P_i = Mv + u \, dm$$ $$P_f = (M + dm)(v + dv)$$ $$\Delta P = M \, dv + (v - u) \, dm$$ $$F = \frac{dP}{dt} = M \frac{dv}{dt} + (v - u) \frac{dm}{dt}$$ $$F = u \frac{dm}{dt} = \rho A u^2$$ from conservation of momentum , the cannon recoils with the same force which it applies. $$\quad \frac{dm}{dt}...
View full post »

Similar threads

Friction problem of a block sandwiched between 2 surfaces
Replies
6
Views
1K
Newton's law problem: Pushing 2 stacked blocks on a horizontal table
Replies
13
Views
3K
Block sliding on a semicircular track with friction
Replies
10
Views
2K
Dynamics of a Block on top of a slab with friction between them
Replies
33
Views
1K
Why can we move the spring with constant speed when we apply a force?
Replies
29
Views
2K
Why Does the Friction Force Not Match in the Two Block Problem?
Replies
15
Views
3K
A block of mass m is dropped onto the top of a vertical spring....
Replies
8
Views
5K
Coefficient of Friction question for a cart going down a wooden ramp
Replies
18
Views
3K
Force pulling on a string at an angle with a block at the other end
Replies
2
Views
1K
Body attached to a block by a spring, shaped like an inclined plane
Replies
1
Views
952

Hot Threads

Recent Insights

Back
Top