nawand
- 8
- 0
Homework Statement
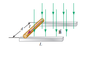
A rod of mass 0.720 kg and radius 6.00 cm rests on two parallel rails fig.1 that are the d=12.0 cm apart and L=45.0 cm long. The rod carries a current of I=48.0 A in the direction shown and rolls along the rails without sleeping. A uniform magnetic field of magnitude 0240 T is directed perpendicular to the rod and the rails. If it starts from rest, what is the speed of the rod as it leaves the rails?
Homework Equations
0+0+Fb *L*cos θ = (mv2)/2 +(Iω2)/2
The Attempt at a Solution
The rod gains energy from the rest, so begin kinetic energy and rotational energy are zero. The only source of energy rod gains is magnetic filed.
I = (mr2)/2
K=(mv2)/2
w=v/r
That is right side of equations becomes:
(mv2)/2 + 1/2 (mv2)+1/2(1/2 mr2) * (v2/r2)
Fb * L = 3/4 mv2
Where
Fb = I * d * B
etc
v=1.07 m/s
Because the force move the rod parallel to the rails along x axis, the dot product will be:
E=Fb * L * cos θ = Fb*L*1=FbL
The question is how do we get the value of energy exerts magnetic field on the rod?
That is force time Length of rails (Fb times L)?
For the electric field is E = qFe