stunner5000pt
- 1,443
- 4
have a look a the diagram
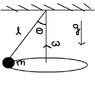
heavy particle of mass m is tied to one end of a string which is of length l. The other end is attached to the ceiling. The particle forms uniform circular motion. Angular velocity of omega. String is angle theta. Ignore friction and mass of string.
Find magnitude of string force S in terms of m, l, omega
horizontal components F_{x} = F sin \theta = m \omega^2 l sin \theta
vertical components = F_{y} = F cos \theta = mg
total components F = m \sqrt{g^2 + \omega^4 l^2 sin^2 \theta)
the textbook however omits the sin theta and the g part which gives F = ml \omega^2
who is right??
heavy particle of mass m is tied to one end of a string which is of length l. The other end is attached to the ceiling. The particle forms uniform circular motion. Angular velocity of omega. String is angle theta. Ignore friction and mass of string.
Find magnitude of string force S in terms of m, l, omega
horizontal components F_{x} = F sin \theta = m \omega^2 l sin \theta
vertical components = F_{y} = F cos \theta = mg
total components F = m \sqrt{g^2 + \omega^4 l^2 sin^2 \theta)
the textbook however omits the sin theta and the g part which gives F = ml \omega^2
who is right??