Split Monomorphisms .... Bland Defn 3.2.2 & Propn 3.2.3 ....

[Math Amateur]

I am reading Paul E. Bland's book "Rings and Their Modules ...

Currently I am focused on Section 3.2 Exact Sequences in $\text{Mod}_R$ ... ...

I need some help in order to fully understand Definition 3.2.2 and Proposition 3.2.3 ...

Definition 3.2.2 and Proposition 3.2.3 read as follows:

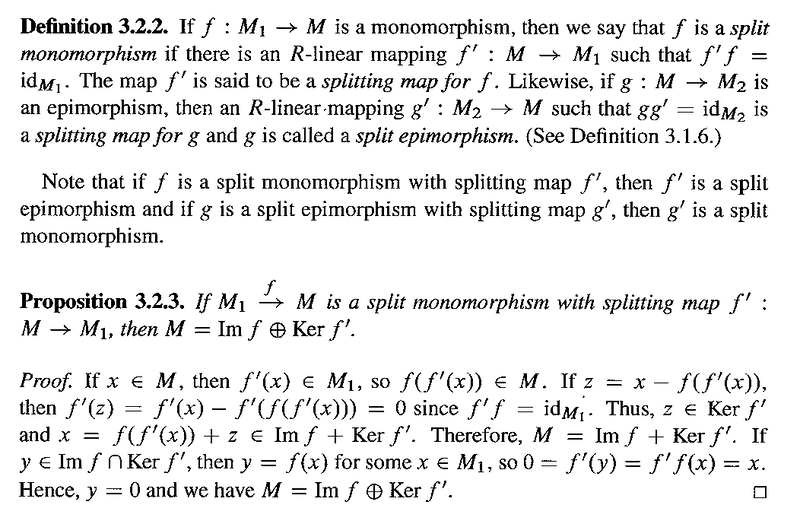
In Definition 3.2.2 we read that $f'f = \text{id}_{M_1}$ ... ... BUT ... ... I thought that $f'f$ was only defined on $f(M) = \text{Im } f$ ... ... what then happens to elements $x \in M$ that are outside of $f(M) = \text{Im } f$ ... ... see Fig. 1 below ...

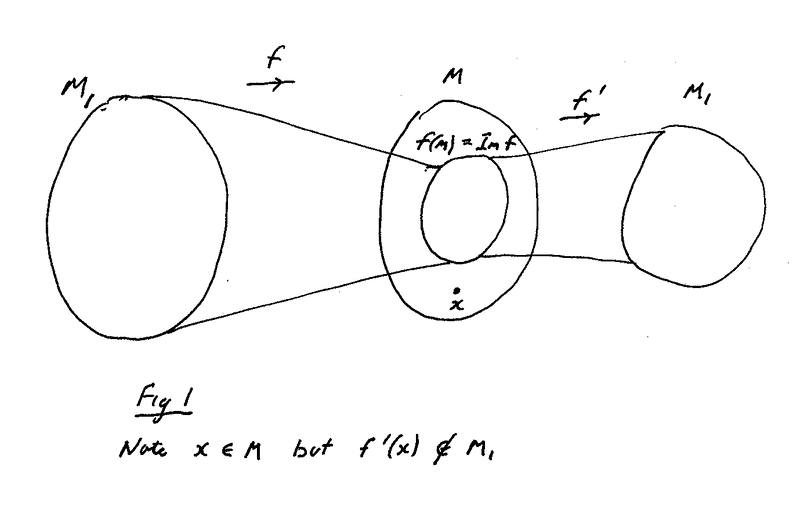
Note that in the proof of Proposition 3.2.3 we read:" ... ... If $x \in M$ then $f'(x) \in M_1$ ... ... "But ... how does this work for $x$ outside of $f(M) = \text{Im } f$ such as $x$ shown in Fig. 1 above?
I would be grateful if someone could explain how Definition 3.2.2 "works" ... ...

Peter

 

[andrewkirk]

$f'$ is described above as having domain $M$ so it is defined on all of $M$, not just on Im$f$

From the Proposition, we see that any $x\in M\smallsetminus f(M_1)$ can be written as $a+b$ where $a\in f(M_1)$ and $b\in\mathrm{ker}\ f'$. So there must be some $m_1\in M_1$ such that $a=f(m_1)$ and we will have

$$f'(x) = f'(a+b) = f'(a) + f'(b) = m_1 + 0_{M_1}=m_1$$

 

[fresh_42]

I would be grateful if someone could explain how Definition 3.2.2 "works" ... ...

The origin are exact sequences (image of the left homomorphism is equal to the kernel of the next). Let's take a short exact sequence. This is a sequence of $R-$module homomorphisms
$$
0 \longrightarrow M_1 \stackrel{f}{\longrightarrow} M \stackrel{g}{\longrightarrow} M_2 \longrightarrow 0 \Longleftrightarrow M_1 \stackrel{f}{\rightarrowtail} M \stackrel{g}{\twoheadrightarrow} M_2
$$
I have a book, in which the author calls such a sequence exact direct, which is a bit more telling, if one the equivalent conditions hold:

1. $\exists \,h: M \longrightarrow M_1 \oplus M_2\, : \,M\cong_h M_1 \oplus M_2$
2. $\exists \,g': M_2 \longrightarrow M \, : \, g \circ g' = \operatorname{id}_{M_2}$
3. $\exists \,f': M \longrightarrow M_1 \, : \, f' \circ f = \operatorname{id}_{M_1}$

This summarizes the situation of Definition 3.2.2.

In general we speak of a split exact sequence, if $g'$ exists which is called the split. The clue is, that $M_1 \stackrel{f}{\rightarrowtail} M_1 \oplus M_2 \stackrel{g}{\twoheadrightarrow} M_2$ always splits AND all splits take this form. So a split describes in a way the possibility to go back in an exact sequence, to embed $M_2$ in $M$. This isn't trivial, because $M_2$ is given as an image, so its structure can be rather wild. A split guarantees that it can be embedded ("backwards") anyway: $g'$ splits $M$ into $M_1$ and $M_2$.

 

[Math Amateur]

The origin are exact sequences (image of the left homomorphism is equal to the kernel of the next). Let's take a short exact sequence. This is a sequence of $R-$module homomorphisms
$$
0 \longrightarrow M_1 \stackrel{f}{\longrightarrow} M \stackrel{g}{\longrightarrow} M_2 \longrightarrow 0 \Longleftrightarrow M_1 \stackrel{f}{\rightarrowtail} M \stackrel{g}{\twoheadrightarrow} M_2
$$
I have a book, in which the author calls such a sequence exact direct, which is a bit more telling, if one the equivalent conditions hold:

1. $\exists \,h: M \longrightarrow M_1 \oplus M_2\, : \,M\cong_h M_1 \oplus M_2$
2. $\exists \,g': M_2 \longrightarrow M \, : \, g \circ g' = \operatorname{id}_{M_2}$
3. $\exists \,f': M \longrightarrow M_1 \, : \, f' \circ f = \operatorname{id}_{M_1}$

This summarizes the situation of Definition 3.2.2.

In general we speak of a split exact sequence, if $g'$ exists which is called the split. The clue is, that $M_1 \stackrel{f}{\rightarrowtail} M_1 \oplus M_2 \stackrel{g}{\twoheadrightarrow} M_2$ always splits AND all splits take this form. So a split describes in a way the possibility to go back in an exact sequence, to embed $M_2$ in $M$. This isn't trivial, because $M_2$ is given as an image, so its structure can be rather wild. A split guarantees that it can be embedded ("backwards") anyway: $g'$ splits $M$ into $M_1$ and $M_2$.

Thanks for the help fresh_42 ...

But just a clarification ...

You write:

"... ... In general we speak of a split exact sequence, if $g'$ exists which is called the split. The clue is, that $M_1 \stackrel{f}{\rightarrowtail} M_1 \oplus M_2 \stackrel{g}{\twoheadrightarrow} M_2$ always splits AND all splits take this form. ... ... "

Can you explain the meaning of the special arrows under the f and under the g in $M_1 \stackrel{f}{\rightarrowtail} M_1 \oplus M_2 \stackrel{g}{\twoheadrightarrow} M_2$ ... ?Thanks again,

Peter

 

[Math Amateur]

$f'$ is described above as having domain $M$ so it is defined on all of $M$, not just on Im$f$

From the Proposition, we see that any $x\in M\smallsetminus f(M_1)$ can be written as $a+b$ where $a\in f(M_1)$ and $b\in\mathrm{ker}\ f'$. So there must be some $m_1\in M_1$ such that $a=f(m_1)$ and we will have

$$f'(x) = f'(a+b) = f'(a) + f'(b) = m_1 + 0_{M_1}=m_1$$

Thanks Andrew ...

Appreciate the help ...

Peter

 

[fresh_42]

Can you explain the meaning of the special arrows under the $f$ and under the $g$ in $M_1 \stackrel{f}{\rightarrowtail} M_1 \oplus M_2 \stackrel{g}{\twoheadrightarrow} M_2$ ... ?

Yes. I said that $M_1 \stackrel{f}{\rightarrowtail} M_1 \oplus M_2 \stackrel{g}{\twoheadrightarrow} M_2$ is equivalent to the short exact sequence
$$0 \stackrel{\iota}{\longrightarrow} M_1 \stackrel{f}{\longrightarrow} M = M_1 \oplus M_2 \stackrel{g}{\longrightarrow} M_2 \stackrel{\pi}{\longrightarrow} 0$$
So the sequence is exact at $M_1$ which means $0 =\operatorname{im}\iota = \operatorname{ker} f$, i.e. $f$ is injective. $M_1 \rightarrowtail M$ represents an injective homomorphism, an embedding.
And the sequence is exact at $M_2$ which means $\operatorname{im} g = \operatorname{ker} \pi = M_2$, i.e. $g$ is surjective. $M \twoheadrightarrow M_2$ represents a surjective homomorphism, a projection.

The notation with the special arrows simply avoids the need to note the zero modules at the left and at the right and can be used in general to denote injective $\rightarrowtail$, resp. surjective $\twoheadrightarrow$ mappings. If you use both at the same time, then it symbolizes a bijection. Unfortunately, I haven't found the LaTeX code for $M \twoheadrightarrowtail M_1 \oplus M_2$