Spring-Block Work Done

[Puneet Tanwar]

Hi - I'm looking for some help with the solution of this problem

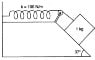
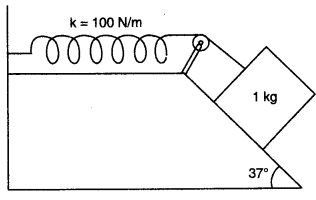
"A 1 kg block situated on a rough incline is connected to a spring with spring constant 100 Nm-1 as shown in Figure. The block is released from rest with the spring in the unstretched position. The block moves 10 cm down the incline before coming to rest. Find the coefficient of friction between the block and the incline. Assume that the spring has negligible mass and the pulley is friction less."

The solution given is :

I tried to solve the problem based on the final equilibrium state - without calculating the work done. The equations I end up with are:

Block: mg sin θ = µ mg cos θ + T
Spring end: T = kx

Leading to : mg (sin θ - µ cos θ) = kx

This is off by factor of 2 compared to the solution above.

What's the right approach to solve the problem?

 

[stockzahn]

Block: mg sin θ = µ mg cos θ + T

Unfortunately, that's a wrong assumption in this scenario. The friction force is a reaction force. Imagine $\mu$ to have exactely a value, so that the block stops at a position $x$ for which $kx=mg\;sin \theta$. Then the two forces are in equilibrium, the block does not move and no friction force is acting on it. Therefore your approach in this case is not applicable.

 

[Puneet Tanwar]

Unfortunately, that's a wrong assumption in this scenario. The friction force is a reaction force. Imagine $\mu$ to have exactely a value, so that the block stops at a position $x$ for which $kx=mg\;sin \theta$. Then the two forces are in equilibrium, the block does not move and no friction force is acting on it. Therefore your approach in this case is not applicable.

Understood. Thanks!