MATLAB Spring mass impact system in Matlab - How to correct it?

[k.udhay]

TL;DR Summary

A mass of constant velocity colliding on spring is modeled in simulink. Result expected was to be of sinusoidal displacement of spring. However result found was different.

I am new to Simulink and I wanted to start practicing using a spring mass damper system. My first tutorial was this:



Later, I wanted to model a spring system where a mass moving at a known velocity hits the spring. The governing equation and a similar modeling method given in the previous youtube link was also prepared:

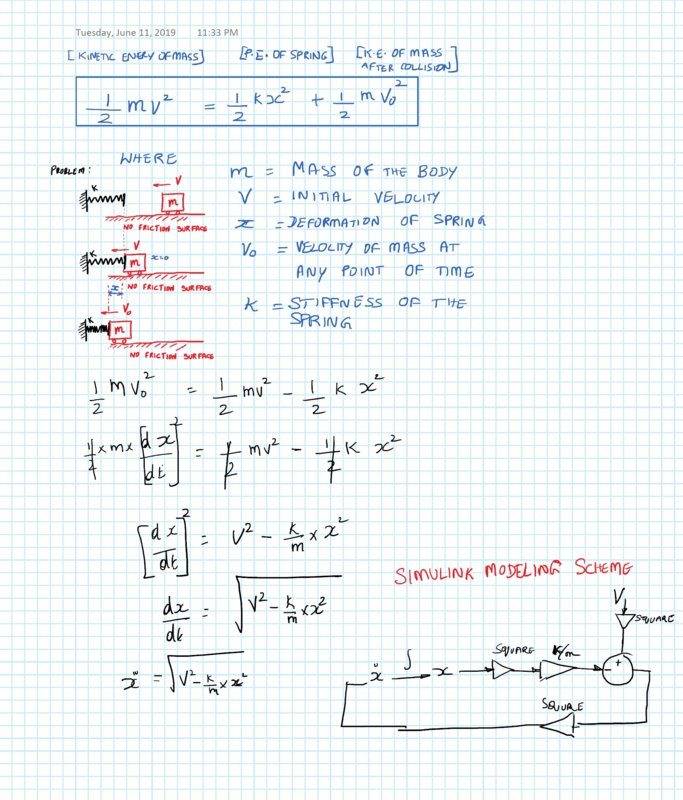Here is the Matlab Simulink model:
https://1drv.ms/u/s!AiW7GXWiq-LLgitdmZqU4QhFeVU5?e=PiZxp3

The result I expected was a sinusoidal displacement of the spring. However the result was totally different:

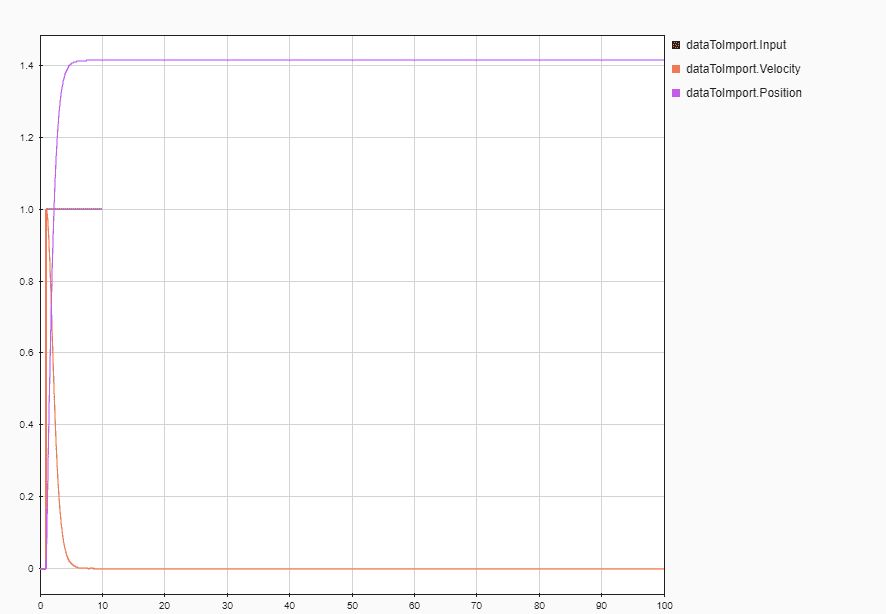
If someone can tell what exactly is my mistake and the correction, that will be of huge help. Thanks.

 

[RPinPA]

You're using an energy equation where all the terms are positive. It is not going to tell you the signs of $x$ or of $v$.

To get the equation of motion, you want to use the fact that the force on the mass is related to the displacement $F = -kx = m \frac {d^2x}{dt^2}$ This force will change sign as $x$ changes sign, which will lead to the sinusoidal behavior.

 

[RPinPA]

Please update at some point and let me know if my observation actually led to success. It was just something that jumped out at me looking at your equation.

 

[k.udhay]

Thank you for your inputs, RPinPA. While I understand force based equation will give me sinusoidal displacement output (as mentioned in the youtube link in OP), I have two questions that I need a clarity:

1. Why will the energy based governing equation not give correct displacement values? It involves velocity (which is a derivative of position) too.

2. If I go with force based governing equation (as you have suggested), where do I input the initial velocity of the mass? This is critical as this determines the amount of deformation of spring (= amplitude of sine wave)

 

[RPinPA]

Thank you for your inputs, RPinPA. While I understand force based equation will give me sinusoidal displacement output (as mentioned in the youtube link in OP), I have two questions that I need a clarity:

1. Why will the energy based governing equation not give correct displacement values? It involves velocity (which is a derivative of position) too.

Because you can't tell whether to take the velocity as positive or negative at any given time. Both are solutions.

2. If I go with force based governing equation (as you have suggested), where do I input the initial velocity of the mass? This is critical as this determines the amount of deformation of spring (= amplitude of sine wave)

Well if you were solving this analytically, you'd have a functional expression for $x(t)$ with some free parameters and you'd evaluate its derivative at $t = 0$ to use the information on $v(0)$.

I don't know much about Simulink but I assume you are implementing differential equations and the software takes care of evolving a solution numerically from starting conditions. So here's a more convenient form for that.

A common transformation of 2nd order equations is to turn it into a system of 1st order equations.
So we have this:
$$-kx = m\frac {d^2x}{dt^2}$$

Change it to this equivalent system in the two variables $v$ and $x$:
$$\frac {dx}{dt} = v \\
m\frac {dv}{dt} = -kx$$
Implement those two equations in those two unknowns with the desired initial conditions on $x$ and $v$.

 

[RPinPA]

I should emphasize that my comments are about the mathematics of the differential equations you're solving, as I have no expertise in Simulink. I have used Matlab for decades but managed to avoid ever using Simulink or even having it on a computer I was using.

 

[k.udhay]

Thanks a lot. I will try this and update you.

 

[k.udhay]

@RPinPA - I tried this in Simulink and there is actually a progress:

However, I see some form of dampening effect in all position, velocity and acceleration plots. I am unable to understand the reason for this. This is my simulink model:

The initial condition (40) tells that dx/dt = 40 when t = 0. I am not very sure if this way of inputting is right. I will be so glad if someone of PF helped me out of this issue. Thank you for guiding me very closely.