Spring pendulum with and without weight

[Stuka_Hunter]

Homework Statement

Weight, the mass of which is 4,9 kg, hangs on a spring which is swinging with a period time of 0,5 seconds. For how much does a spring shorten, when weight is removed?

Relevant Equations

Equations are stated below

Equations provided:

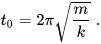for a spring pendulum and m replaced with L and k with g for the same pendulum, but with no weight attached.

Greetings

I tried solving this by stating that the length is 0,50m (since no length of the spring is given) and turning around the equation for the spring coefficient (k), from which i got 0,18 as the coefficient. Can someone confirm this is the correct result? Even though it looks right, I doubt it is correct, because when i put it into the original equation, i get a period time of 32 seconds...

Any help is appreciated :)

 

[kuruman]

If you have a vertical spring of constant $k$ and you hang mass $m$ from it, by how much extra distance does the spring stretch? Draw a free body diagram. Should you need additional help, please show all your work, not just the answer you got. Thanks.