- #1
fab13
- 312
- 6
Hello,
I'am studying a code (called "starscream") which allows to make initial conditions (positions and velocities) for NBody simulation. They are based on Springel and White (1999) model. I have several problems about the underlying equations used in this code.
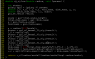
Firstly, See attachment "fig1.png", for computing the disk scale length, into the "disk_scale_length_func" routine, the author seems to have forgotten to multiply the line 128 by the line 129, i.e the
factor "sqrt(1.0/f_c_func(gal->halo_concentration))".
Indeed, the definition of the disk scale length is :
[tex]
R_{d}=\dfrac{1}{\sqrt{2}}\,\bigg(\dfrac{j_{d}}{m_{d}}\bigg)\,\lambda\,r_{200}\,f_{c}^{-1/2}\,f_{R}(\lambda,c,m_{d},j_{d})
[/tex]
where [tex] f_{R}(\lambda,c,m_{d},j_{d})=2\bigg[\int_{0}^{\infty}\,e^{-u}\,u^{2}\,\dfrac{v_{c}(R_{d}\,u)}{v_{200}}\,du\bigg]^{-1}[/tex]
and [tex] f_{c}=\dfrac{c}{2}\,\dfrac{1-1/(+c)^{2}-2\,(ln(1+c))/(1+c)}{[c/(1+c)-ln(1+c)]^{2}} [/tex]
Here is the original part of this code :
Is anyone can confirm this error ?
------------------------------------------------------------------------------------------------------------------------------------------------
Secondly, See attachment "fig2.png", into the "dj_d_func" routine, I don't understand the lines 199 to 201. Actually, from this equation in the doc :
[tex]
v_{c}^{2}(R)=R\,\dfrac{\partial\Phi}{\partial
R}=4\pi\,G\,\Sigma_{0}\,\dfrac{R^{2}}{4\,R_{d}}\,\bigg[I_{0}\,\bigg(\dfrac{R}{2\,R_{d}}\bigg)\,K_{0}\,\bigg(\dfrac{R}{2\,R_{d}}\bigg)+I_{1}\,\bigg(\dfrac{R}{2\,R_{d}}\bigg)\,K_{1}\,\bigg(\dfrac{R}{2\,R_{d}}\bigg)\bigg]
[/tex] (eq 1)
this should be :
[tex]
v_{c}^{2}=\dfrac{GM_{d}(r)}{r} \rightarrow M_{d}(r)=\dfrac{v_{c}^{2}\,r}{G}
[/tex]
with [tex]v_{c}^{2}[/tex] computed from the (eq 1) equation.
The mass density of the disk is :
[tex]
\Sigma(R)=\Sigma_{0}\,e^{-R/R_{d}}=\dfrac{M_{d}}{2\pi\,R_{d}^{2}}\,e^{-R/R_{d}}
[/tex] (eq 2)
With the expression of [tex]\Sigma_{0}[/tex] on (eq 2), we can have :
[tex]
M_{d}(r)=\dfrac{v_{c}^{2}\,r}{G}=M_{d,total}\,\dfrac{R^{3}}{2\,R_{d}^{3}}\,\bigg[I_{0}\,\bigg(\dfrac{R}{2\,R_{d}}\bigg)\,K_{0}\,\bigg(\dfrac{R}{2\,R_{d}}\bigg)+I_{1}\,\bigg(\dfrac{R}{2\,R_{d}}\bigg)\,K_{1}\,\bigg(\dfrac{R}{2\,R_{d}}\bigg)\bigg]
[/tex]
So into the code, on line 199, with [tex]y=R/(2\,R_{d})[/tex] and we should have :
disk_mass=4*total_mass_disk*y*y*y*(I_{0}*K_{0}+I_{1}*K_{1})
and not only one product "y*y".
Here is the original part of this code (with in bold my correction) :
Is my modification correct ?
I make you notice too that there is a minus sign on the original code at line 199 : (I_{0}*K_{0} - I_{1}*K_{1}) : is this good ?
Thanks for your help
I'am studying a code (called "starscream") which allows to make initial conditions (positions and velocities) for NBody simulation. They are based on Springel and White (1999) model. I have several problems about the underlying equations used in this code.
Firstly, See attachment "fig1.png", for computing the disk scale length, into the "disk_scale_length_func" routine, the author seems to have forgotten to multiply the line 128 by the line 129, i.e the
factor "sqrt(1.0/f_c_func(gal->halo_concentration))".
Indeed, the definition of the disk scale length is :
[tex]
R_{d}=\dfrac{1}{\sqrt{2}}\,\bigg(\dfrac{j_{d}}{m_{d}}\bigg)\,\lambda\,r_{200}\,f_{c}^{-1/2}\,f_{R}(\lambda,c,m_{d},j_{d})
[/tex]
where [tex] f_{R}(\lambda,c,m_{d},j_{d})=2\bigg[\int_{0}^{\infty}\,e^{-u}\,u^{2}\,\dfrac{v_{c}(R_{d}\,u)}{v_{200}}\,du\bigg]^{-1}[/tex]
and [tex] f_{c}=\dfrac{c}{2}\,\dfrac{1-1/(+c)^{2}-2\,(ln(1+c))/(1+c)}{[c/(1+c)-ln(1+c)]^{2}} [/tex]
Here is the original part of this code :
Code:
// This function determines the scale length of the disk to within 15% or so using
// the fitting formula provided in MMW97.
double disk_scale_length_func(galaxy *gal) {
int i;
double base, power, c, f_conc, f, scale, old_scale, v_c;
c = gal->halo_concentration;
f_conc = 2.0/3.0+ pow((c/21.5),0.7);
base = (gal->j_d*gal->lambda)/(0.1*gal->m_d);
power = (-0.06+2.71*gal->m_d+0.0047*gal->m_d/(gal->j_d*gal->lambda));
f = pow(base,power)*(1.0-3.0*gal->m_d+5.2*gal->m_d*gal->m_d) *
(1.0-0.019*c+0.00025*c*c+0.52/c);
gal->disk_scale_length = (1.0/sqrt(2.0))*(gal->j_d/gal->m_d)*gal->lambda*
gal->r200*(f/sqrt(f_conc));
// Now try to iterate for the correct value.
for (i = 0; i < 50; ++i) {
scale = sqrt(1.0/2.0)*(gal->j_d/gal->m_d)*gal->lambda*gal->r200*
[B]2.0*(gal->v200/j_d_func(gal)) // product missing "*" with the next line
sqrt(1.0/f_c_func(gal->halo_concentration));[/B]
gal->disk_scale_length = scale;
printf("scale = %f\n",scale);
}
return scale;
}Is anyone can confirm this error ?
------------------------------------------------------------------------------------------------------------------------------------------------
Secondly, See attachment "fig2.png", into the "dj_d_func" routine, I don't understand the lines 199 to 201. Actually, from this equation in the doc :
[tex]
v_{c}^{2}(R)=R\,\dfrac{\partial\Phi}{\partial
R}=4\pi\,G\,\Sigma_{0}\,\dfrac{R^{2}}{4\,R_{d}}\,\bigg[I_{0}\,\bigg(\dfrac{R}{2\,R_{d}}\bigg)\,K_{0}\,\bigg(\dfrac{R}{2\,R_{d}}\bigg)+I_{1}\,\bigg(\dfrac{R}{2\,R_{d}}\bigg)\,K_{1}\,\bigg(\dfrac{R}{2\,R_{d}}\bigg)\bigg]
[/tex] (eq 1)
this should be :
[tex]
v_{c}^{2}=\dfrac{GM_{d}(r)}{r} \rightarrow M_{d}(r)=\dfrac{v_{c}^{2}\,r}{G}
[/tex]
with [tex]v_{c}^{2}[/tex] computed from the (eq 1) equation.
The mass density of the disk is :
[tex]
\Sigma(R)=\Sigma_{0}\,e^{-R/R_{d}}=\dfrac{M_{d}}{2\pi\,R_{d}^{2}}\,e^{-R/R_{d}}
[/tex] (eq 2)
With the expression of [tex]\Sigma_{0}[/tex] on (eq 2), we can have :
[tex]
M_{d}(r)=\dfrac{v_{c}^{2}\,r}{G}=M_{d,total}\,\dfrac{R^{3}}{2\,R_{d}^{3}}\,\bigg[I_{0}\,\bigg(\dfrac{R}{2\,R_{d}}\bigg)\,K_{0}\,\bigg(\dfrac{R}{2\,R_{d}}\bigg)+I_{1}\,\bigg(\dfrac{R}{2\,R_{d}}\bigg)\,K_{1}\,\bigg(\dfrac{R}{2\,R_{d}}\bigg)\bigg]
[/tex]
So into the code, on line 199, with [tex]y=R/(2\,R_{d})[/tex] and we should have :
disk_mass=4*total_mass_disk*y*y*y*(I_{0}*K_{0}+I_{1}*K_{1})
and not only one product "y*y".
Here is the original part of this code (with in bold my correction) :
Code:
double dj_d_func(double radius, void *params) {
int status;
galaxy *gal = (galaxy *) params;
double I_0, K_0, I_1, K_1, halo_mass, disk_mass, y, a;
double total_disk_mass, v_c, scale;
gsl_sf_result result;
scale = gal->disk_scale_length;
total_disk_mass = gal->disk_mass;
a = gal->halo_a_value;
halo_mass = gal->halo_mass;
y = radius/(2.0*scale);
status = gsl_sf_bessel_I0_e(y,&result);
I_0 = result.val;
status = gsl_sf_bessel_K0_e(y,&result);
K_0 = result.val;
status = gsl_sf_bessel_I1_e(y,&result);
I_1 = result.val;
status = gsl_sf_bessel_K1_e(y,&result);
K_1 = result.val;
[B] // ORIGINAL VERSION
disk_mass = 2.0*total_disk_mass*y*y*(I_0*K_0 - I_1*K_1);
// END ORIGINAL VERSION[/B]
[B] //THIS SHOULD BE
//disk_mass = 4.0*total_disk_mass*y*y*y*(I_0*K_0 + I_1*K_1);
// END CORRECTION[/B]
halo_mass = halo_mass*radius*radius/((radius+a)*(radius+a));
v_c = sqrt(G*(halo_mass/(radius*kpc) + disk_mass/(scale*kpc)));
return v_c*(radius/scale)*(radius/scale)*exp(-radius/scale);
}Is my modification correct ?
I make you notice too that there is a minus sign on the original code at line 199 : (I_{0}*K_{0} - I_{1}*K_{1}) : is this good ?
Thanks for your help