Squeeze Mapping: Transform Circle to Quarter Moon Shape

[Carol_m]

Hello!

I am trying to transform a circle into a "quarter moon shape". This is that every point in the circle is mapped into the "quarter moon shape" - therefore squeezed.

In particular I am looking for a expression that relates x x' and y y' ...

Can any bright mind help me :) ?

Thank you

 

[henry_m]

I'm not quite sure exactly what you mean by a "quarter moon", can you be any more explicit? In any case, there will be a whole multitude of such mappings; do you want some specific property (perhaps conformality like your other thread)?

It'd be useful if you could give some context to your question, then perhaps I can be a little more helpful. Why are you interested in this expression?

 

[Carol_m]

Hi henry_m,

Please check the figure attached so you can see what I meant about the "quarter moon" shape. Sorry if I wasn't clear, I didn't know how to call it :)

I am an engineer and this is part of a problem that I need to solve. Basically, I want to map every point in the circle to a point in the "quarter moon" shape. In my understanding y'=y but I am struggling to get x' in terms of x.

Any help from the bright minds is much appreciate it! :)

Thank you!

 

[coelho]

Ok... the attached figure shows what this mapping must do. It must map each (red) line of the circle to a line of the quarter moon. Let's see how it can be done.

The equation of a circle of radius r is:

x^2+y^2=r^2

so, the x coordinate of left half of the circle (which i will call xL) is given by:

x_L=-\sqrt{r^2-y^2}

and the x coordinate of the right half of the circle is:

x_R=\sqrt{r^2-y^2}

Which means the ends of the red line on the circle are at the coordinates (xL,y) and (xR,y).

The right half of the quarter moon is a half circle, so its x coordinate (which i will call x'R) is also given by:

x'_R=\sqrt{r^2-y^2}

The left half of the quarter moon is exactly midway between the right half and the y axis, so its x coordinate (which i will call x'L) is the half of x'R:

x'_L=\frac{\sqrt{r^2-y^2}}{2}

And so the coordinates of the ends of the red line on the quarter moon are (x'L,y) and (x'R,y).

Now we just need to find a transformation that map points on the red line on the circle to points on the quarter moon. If we choose a linear transformation:

x'=Ax+B

It must map the left end of the red line on the circle (at (xL,y)) to the left end of the red line on the quarter moon (at (x'L,y)), so the following must be true:

x'_L=Ax_L+B.

It must also be true for the right ends of both lines, so:

x'_R=Ax_R+B.

Solving it for A and B and substituting the values of xL, xR, x'L and x'R, we find:

A=\frac{1}{4}

and

B=\frac{3\sqrt{r^2-y^2}}{4}

So, the final transformation is:

x'=\frac{1}{4}x+\frac{3\sqrt{r^2-y^2}}{4}.

 

[henry_m]

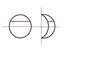
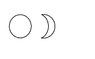OK, I guess that the left-hand boundary of that figure is the arc of a larger circle, intersecting the smaller one at opposite points?

One strategy would certainly be to keep y the same, and then for each fixed y just map linearly, i.e keep each point the same proportional distance away from the left and right boundaries. So, explicitly, if the left and right boundaries on the original figure are at x=f₁(y) and g₁(y) repectively, and on the final figure at x=f₂(y) and g₂(y) (in your example g₁=g₂), you have a map (x',y')=(a(y)x+b(y),y), with a(y) and b(y) chosen such that (f₁(y),y) maps to (f₂(y),y) and similar for g.

I hope that's clear. The rest should be just algebra, though it might be a little messy.

Another way that is perhaps mathematically a little prettier is to find a conformal map using complex variables. My strategy would be find the inverse map. First translate so one of the corners is at 0, then take z-->1/z, which will leave you with a 'wedge'. Translate again so that the corner of the wedge is at the origin, then take some power to turn it into a half-plane. Then a standard mobius map will take you to a circle. Depending on your application, this is likely to be seriously messy though, especially if you write it in terms of (x,y)-->(x',y') rather than z-->z', and I wouldn't like to have to do all this explicitly, at least without mathematica to help me out.

 

[Carol_m]

Hi coelho!

Thank you very much for your detailed response it has been really useful!

many thanks to henry_m too for the help!

You guys are great!

Cheers,