Here seems to be a lot of unnecessary confusion. Of course, electrodynamics can be written in manifest covariant form. It's a Poincare invariant local classical field theory and as such can be formulated with Minkowski tensors (I restrict myself to special relativity here). To see this, we start with the usual non-covariant formalism (although it can be made also covariant, using the Silberstein-vector representation, but that's an advanced topic) 1+3-D formalism in a fixed inertial reference. I use Heaviside-Lorentz units, which are the most convenient and natural ones in the context of relativistic electromagnetics. The homogeneous Maxwell equations read
$$\vec{\nabla} \cdot \vec{B}=0, \quad \vec{\nabla} \times \vec{E}+\frac{1}{c} \partial_t \vec{B}=0.$$
From the first equation we see that (at least locally) there exists a vector potential, ##\vec{A}## such that
$$\vec{B}=\vec{\nabla} \times \vec{A}.$$
Plugging this in the 2nd equation gives
$$\vec{\nabla} \times \left ( \vec{E}+\frac{1}{c} \partial_t \vec{A} \right)=0,$$
and thus the field in the parenthesis is (at least locally) a gradient field
$$\vec{E}=-\vec{\nabla} A^0 - \frac{1}{c} \partial_t \vec{A}.$$
Now I've already written ##A^0## for the scalar potential, which is suggestive for putting ##(A^0,\vec{A})## together as components of a Minkowski four-vector field, ##A^{\mu}##. Now we have to check whether the inhomogeneous Maxwell equations are compatible with that.
We first note that the charge density and current density can be put into a four-vector field,
$$(j^{\mu})=(c \rho,\vec{j}).$$
Indeed we can write for a charged-particle flow ##\vec{v}##,
$$(j^{\mu})= \rho (c,\vec{v})=\frac{\rho}{\gamma} c (\gamma,\gamma \vec{\beta})=\rho_0 c (u^{\mu}),$$
where
$$\vec{\beta}=\frac{\vec{v}}{c}, \quad \gamma=\frac{1}{\sqrt{1-\vec{\beta}^2}}.$$
Now ##\rho_0## is the density in the (local) restframe of the fluid cell and as such a scalar, while the four-velocity
$$(u^{\mu})=\gamma (1,\vec{\beta})$$
is a four-vector field, and thus ##(j^{\mu})## is indeed a four-vector field.
Now let's see what the inhomogeneous Maxwell equations tell. In (1+3) form they read
$$\vec{\nabla} \cdot \vec{E}=\rho=\frac{1}{c} j^0, \quad -\frac{1}{c} \partial_t \vec{E}+\vec{\nabla} \times \vec{B}=\frac{1}{c} \vec{j}.$$
To see that these are in fact Poincare-covariant equations, we plug in the potentials and use ##x^0=ct##,
$$\vec{\nabla} \cdot (\vec{\nabla} A^0+\partial_0 \vec{A} )=(\Delta A^0+\partial_0 \partial_i A^i)=-\frac{1}{c} j^0.$$
Now
$$\Delta = \sum_i \partial_i \partial_i=-\partial^i \partial_i,$$
and thus
$$(\partial_i (\partial^i A^0-\partial^0 A^i)=+\frac{1}{c} j^0.$$
This suggests to introduce the antisymmetric Faraday tensor,
$$F^{\mu \nu}=\partial^{\mu} A^{\nu}-\partial^{\nu} A^{\mu} \; \Rightarrow \; \partial_i (\partial^i A^0-\partial^0 A^i) = \partial_{\mu} F^{0 \mu}=\frac{1}{c} j^0. \qquad (*)$$
Now it's clear that we must get also the Maxwell-Ampere law in terms of ##F^{\mu \nu}##. Indeed plugging in the potentials gives
$$-\partial_0 (-\partial_0 \vec{A}-\vec{\nabla} A^0)+\vec{\nabla} \times (\vec{\nabla} \times \vec{A})=\frac{1}{c} \vec{j}.$$
Using
$$\vec{\nabla} \times(\vec{\nabla} \times \vec{A})=\vec{\nabla} (\vec{\nabla} \cdot \vec{A})-\Delta \vec{A},$$
written in terms of components we get
$$\partial_0 (\partial^0 A^i - \partial^i A^0) + \partial_j (-\partial^i A^j+\partial^{j}A^i)=\frac{1}{c} j^i$$
or with the Faraday-tensor components
$$\partial_0 F^{0i}+\partial_j F^{ji}=\partial_{\mu} F^{\mu i} =\frac{1}{c} j^i.$$
Together with (*) we thus have also the inhomoegenous Maxwell equations covariant form
$$\partial_{\mu} F^{\mu \nu}=\Box A^{\nu} -\partial^{\nu} \partial_{\mu} A^{\mu}=\frac{1}{c} j^{\nu} \quad \text{with} \quad \Box = \partial_{\mu} \partial^{\mu}.$$
You can use gauge invariance to simplify the equation for the four-vector potential by imposing the Lorenz gauge condition,
$$\partial_{\mu} A^{\mu}=0,$$
leading to
$$\Box A^{\mu}=\frac{1}{c} j^{\mu}.$$
For a free field, ##j^{\mu}=0##, the plane-wave solution reads
$$A^{\mu}=a^{\mu} \exp(-\mathrm{i} k \cdot x)$$,
where ##a^{\mu}=\text{const}## and ##k=(k^{\mu})=\text{const}##. From ##\Box A^{\mu}=0## one finds
$$k_{\mu} k^{\mu}=0$$
and from the Lorentz-gauge condition
$$k_{\mu} a^{\mu}=k \cdot a=0.$$
The gauge is still not completely fixed, because you can change to another vector potential by
$$A_{\mu}'=A_{\mu} +\partial_{\mu} \chi$$
with an arbitrary scalar field ##\chi## which obeys the wave equation ##\Box \chi=0## without violating the Lorenz-gauge condition. This can be used to arbitrarily set ##a^0=0## ("radiation gauge"), and you are left with two independent components for ##a^{\mu}=(0,\vec{a})## subject to the transversality condition ##\vec{k} \cdot \vec{a}=0##.
Now as any other vector field ##A^{\mu}## tansforms under LT's as
$$\bar{A}^{\mu}(\bar{x})={\Lambda^{\mu}}_{\rho} A^{\rho}(x).$$
Thus we have
$$\bar{k}=\hat{\Lambda} k,$$
which includes the Doppler and aberration effect in compact form.
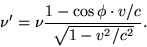In this Wiki article, the same formula is derived.
