Whatupdoc
- 99
- 0
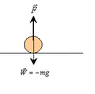
A Standing Vertical Jump. Basketball player Darrell Griffith is on record as attaining a standing vertical jump of 1.2 m (4 ft). (This means that he moved upward by 1.2 m after his feet left the floor.) Griffith weighed 890 N (200 lb).
1.) Use Newton's laws and the results of part (B) to calculate the average force he applied to the ground. F= m*a
ok i really don't know how to do this. i know that there is a force of 890 N that is already given. and the acceleration that i found from part b, which is below. if i plugged it in, i would find the mass, which is useless(i think).
can someone point me to the right direction? just a guess, but i just think it's 890N cause that's the force that he has.
this is part b.) If the time of the part of the jump before his feet left the floor was 0.300 s, what was the magnitude of his average acceleration while he was pushing against the floor? Results of part b is 16.2 m/s^2
1.) Use Newton's laws and the results of part (B) to calculate the average force he applied to the ground. F= m*a
ok i really don't know how to do this. i know that there is a force of 890 N that is already given. and the acceleration that i found from part b, which is below. if i plugged it in, i would find the mass, which is useless(i think).
can someone point me to the right direction? just a guess, but i just think it's 890N cause that's the force that he has.
this is part b.) If the time of the part of the jump before his feet left the floor was 0.300 s, what was the magnitude of his average acceleration while he was pushing against the floor? Results of part b is 16.2 m/s^2