Starting an electrostatic cylinder problem

[Blastrix91]

Homework Statement

http://img842.imageshack.us/img842/2816/unavngivettz.png

My problem is that I'm confused about a hint I was given in this problem. I usually use the law of cosine to find the length of $\vec{r}-\vec{r'}$ in sphere problems. But the hint I have says that I should make it $[r^2 + (z - z_0)^2]^{1/2}$

Where could this be coming from? I can't quite get my head around the geometrical idea of this hint. Can't the law of cosine be used here?

($\vec{r'}$ is the vector to the charge distribution. $\vec{r}$ is the vector to everywhere in space, but since it is the potential at the axis of the cylinder it is probably what is described as z_0.)

I have a hard time seeing where there is any right triangle here to use pythagoras approach on.

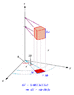
(Here is a illustration of the problem:
http://img820.imageshack.us/img820/3168/unavngivetwj.png )

Homework Equations

The volume part of this equation:
http://img571.imageshack.us/img571/1306/unavngivetmg.png

The Attempt at a Solution

I'm having trouble starting the problem.

 

[TSny]

I usually use the law of cosine to find the length of $\vec{r}-\vec{r'}$ in sphere problems. But the hint I have says that I should make it $[r^2 + (z - z_0)^2]^{1/2}$

Where could this be coming from?

I think the hint is based on using "cylindrical coordinates" $(r, \theta, z)$ where $r$ is the horizontal distance from the z-axis to the element of charge